题目内容
【题目】底面为正方形的四棱锥S﹣ABCD,且SD⊥平面ABCD,SD= ![]() ,AB=1,线段SB上一M点满足
,AB=1,线段SB上一M点满足 ![]() =
= ![]() ,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
【答案】B
【解析】解:以D为坐标原点,以DA,DC,DS为坐标轴建立空间直角坐标系,如图所示:
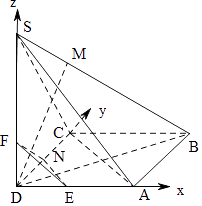
则B(1,1,0),S(0,0, ![]() ),N(0,
),N(0, ![]() ,0),D(0,0,0),M(
,0),D(0,0,0),M( ![]() ,
, ![]() ,
, ![]() ),
),
取AD的中点E,则E( ![]() ,0,0),∴
,0,0),∴ ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0),
∴ ![]() =0,即DM⊥EN,
=0,即DM⊥EN,
在SD上取一点F,设F(0,0,a),则 ![]() =(﹣
=(﹣ ![]() ,0,a),
,0,a),
设DM⊥EF,则 ![]() ,即﹣
,即﹣ ![]() +
+ ![]() =0,解得a=
=0,解得a= ![]() ,
,
∴DM⊥平面EFN,
∴P点轨迹为△EFN.
∵EF=FN= ![]() =
= ![]() ,EN=
,EN= ![]() AC=
AC= ![]() ,
,
∴△EFN的周长为 ![]() =
= ![]() .
.
故选:B.
【考点精析】掌握棱锥的结构特征是解答本题的根本,需要知道侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


