题目内容
15.设x、y∈R,且x2+y2=1,则x+y的最小值是$-\sqrt{2}$.分析 利用三角代换,将圆的普通方程化成圆的参数方程,将x+y表示成cosα+sinα,最后利用辅助角公式进行求解即可.
解答 解:∵x2+y2=1,
∴x=cosα,y=sinα,
则x+y=cosα+sinα=$\sqrt{2}$sin(α+$\frac{π}{4}$),
∴x+y的最小值是$-\sqrt{2}$.
故答案为:$-\sqrt{2}$.
点评 本题主要考查了函数的最值,以及三角代换的方法的运用,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
3.函数值tan224°,sin136°,cos310°的大小关系是( )
| A. | cos310°<sin136°<tan224° | B. | sin136°<cos310°<tan224° | ||
| C. | cos310°<tan224°<sin136° | D. | tan224°<sin136°<cos310° |
20.若f(n)=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2n+1}$(n∈N*),则当n=2时,f(n)是( )
| A. | 1+$\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ | D. | 非以上答案 |
4.对于R上可导的任意函数f(x),若满足(x-2)f′(x)≥0,则必有( )
| A. | f(0)+f(3)<2f(2) | B. | f(0)+f(3)≤2f(2) | C. | f(0)+f(3)≥2f(2) | D. | f(0)+f(3)>2f(2) |
 某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?
某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?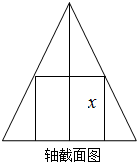 一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:
一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱: