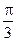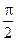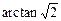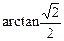题目内容
已知P为△ABC所在平面外的一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点
(1)求EF与PC所成的角;
(2)求线段EF的长.
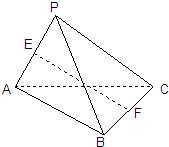
(1)求EF与PC所成的角;
(2)求线段EF的长.

(1)取PB的中点为G,连接FG,EG
∵E、F分别为PA和BC的中点
∴FG∥PC且FG=
PC,EG∥AB且EG=
AB,
∴∠GFE为EF与PC所成的角,∠EGF为PC与AB所成的角
∵PC⊥AB,
∴∠EGF=90°
又EG=GF=1,
∴∠GFE=45°
故EF与PC所成的角为45°;
(2)由(1)知△EGF为Rt△,
∴EF=
=
=
.
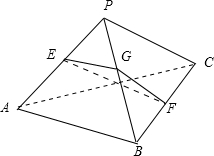
∵E、F分别为PA和BC的中点
∴FG∥PC且FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GFE为EF与PC所成的角,∠EGF为PC与AB所成的角
∵PC⊥AB,
∴∠EGF=90°
又EG=GF=1,
∴∠GFE=45°
故EF与PC所成的角为45°;
(2)由(1)知△EGF为Rt△,
∴EF=
| EG2+FG2 |
| 1+1 |
| 2 |


练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 平面
平面 ,
, ,
, ,
, ,
, ,
, 的大小.
的大小.
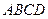 是
是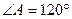 的菱形,绕AC将该菱形折成二面角
的菱形,绕AC将该菱形折成二面角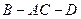 ,记异面直线
,记异面直线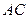 、
、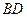 所成角为
所成角为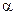 ,
,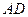 与平面
与平面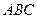 所成角为
所成角为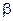 ,当
,当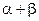 最大时,二面角
最大时,二面角