题目内容

如图，四棱锥S-ABCD的底面是边长为2的正方形，O为底面的中心，SO⊥底面ABCD，SO=
2
，则异面直线CD与SA所成角的大小为______．
∵四棱锥S-ABCD的底面是边长为2的正方形，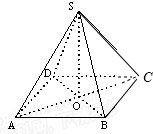
∴AO=BO=
2

∵SO⊥底面ABCD，SO=
2
，
∴SA=SB=2
∵AB=2，∴∠SAB=60°
∵CD∥AB
∴∠SAB（或其补角）为异面直线CD与SA所成角
∴异面直线CD与SA所成角的大小为60°
故答案为：60°．
练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1、CC1的中点,求证:平面EB1D1∥平面FBD.
如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是______．
已知P为△ABC所在平面外的一点，PC⊥AB，PC=AB=2，E、F分别为PA和BC的中点
（1）求EF与PC所成的角；
（2）求线段EF的长．
若直线m与平面α所成角为
π
3
，直线n?α，则直线m，n所成角的取值范围是（　　）
A．(0，
π
2
)		B．[
π
6
，
π
2
]		C．[
π
3
，
π
2
]		D．[
π
6
，
π
3
]
如图：正四面体S-ABC中，如果E，F分别是SC，AB的中点，那么异面直线EF与SA所成的角等于（　　）
A．90°B．45°C．60°D．30°
已知四棱锥P-ABCD的底面是边长为2的菱形，且∠ABC=60°，PA=PC=2，PB=PD．
（Ⅰ）若O是AC与BD的交点，求证：PO⊥平面ABCD；
（Ⅱ）若点M是PD的中点，求异面直线AD与CM所成角的余弦值．
异面直线a，b所成的角为60°，过空间点P作线c与它们都成60°，则线c的条数为______．
已知平面的一条斜线和它在平面内的射影的夹角是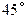，且平面内的直线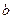和斜线在平面内的射影的夹角是，则直线、所成的角是        （   ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网