题目内容
7.P是平面ABC外一点,PO⊥平面ABC,垂足为O,若PA,PB,PC两辆互相垂直,则O是△ABC的( )| A. | 垂心 | B. | 内心 | C. | 重心 | D. | 外心 |
分析 连结AO并延长,交BC于D,连结BO并延长,交AC于E,由已知条件推导出AD⊥BC,BE⊥AC,由此能证明O是△ABC的垂心.
解答  证明:连结AO并延长,交BC于D,连结BO并延长,交AC于E,
证明:连结AO并延长,交BC于D,连结BO并延长,交AC于E,
∵PA⊥PB,PA⊥PC,∴PA⊥面PBC,∴PA⊥BC,
∵PO⊥面ABC,∴PO⊥BC,∴BC⊥面PAO,
∴AO⊥BC,∴AD⊥BC,
同理,BE⊥AC,
∴O是△ABC的垂心.
故选:A.
点评 本题考查三角形五心的判断,是基础题,解题时要注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
2.已知tanα=2,则$\frac{2sinα+cosα}{sinα-cosα}$=( )
| A. | 2 | B. | 5 | C. | 1 | D. | -1 |
16.己知cos31°=a,则sin239°•tan149°的值是( )
| A. | $\frac{1-{a}^{2}}{a}$ | B. | $\sqrt{1-{a}^{2}}$ | C. | $\frac{{a}^{2}-1}{a}$ | D. | -$\sqrt{1-{a}^{2}}$ |
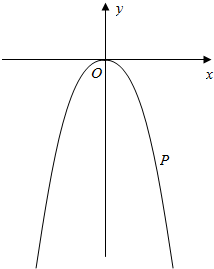 已知抛物线y=-2x2和抛物线上一点P(1,-2).
已知抛物线y=-2x2和抛物线上一点P(1,-2).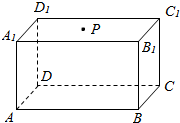 如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l
如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l