题目内容
12.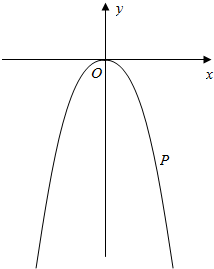 已知抛物线y=-2x2和抛物线上一点P(1,-2).
已知抛物线y=-2x2和抛物线上一点P(1,-2).(Ⅰ)求抛物线的准线方程;
(Ⅱ)过点P作斜率为2,-2的直线l1,l2,分别交抛物线于A(x1,y1),B(x2,y2),设AB的中点M(x0,y0).求证:线段PM的中点Q在
y轴上.
分析 (Ⅰ)利用抛物线方程,可得抛物线的准线方程;
(Ⅱ)确定xQ=0,即可证明结论.
解答 解:(I)抛物线y=-2x2,∴${x^2}=-\frac{1}{2}y$
∴准线方程是$y=\frac{1}{8}$;…4分
(II)直线l1:y-(-2)=2(x-1),即y=2x-4代入y=-2x2,有2x2+2x-4=0,
∴x2+x-2=0,∴x=-2或x=1,即x1=-2…7分
同理直线l2:y-(-2)=-2(x-1),即y=-2x代入y=-2x2,有2x2-2x=0,
∴x2-x=0,∴x=0或x=1,即x2=0…10分
∴${x_0}=\frac{{{x_1}+{x_2}}}{2}=-1$,∴$\frac{{{x_0}+1}}{2}=0$,即xQ=0
即线段PM的中点Q在y轴上.…13分.
点评 本题考查抛物线的方程与性质,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.P是平面ABC外一点,PO⊥平面ABC,垂足为O,若PA,PB,PC两辆互相垂直,则O是△ABC的( )
| A. | 垂心 | B. | 内心 | C. | 重心 | D. | 外心 |