题目内容
1.已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a≥2b>0),则椭圆C的离心率的取值范围是[$\frac{\sqrt{3}}{2}$,1).分析 运用a,b,c 的关系和离心率公式,结合已知不等式,即可得到所求范围.
解答 解:由a≥2b可得a2≥4b2,
又b2=a2-c2,
可得a2≥4a2-4c2,即为4c2≥3a2,
即c≥$\frac{\sqrt{3}}{2}$a,
即有e=$\frac{c}{a}$≥$\frac{\sqrt{3}}{2}$,
由0<e<1,可得$\frac{\sqrt{3}}{2}$≤e<1.
故答案为:[$\frac{\sqrt{3}}{2}$,1).
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率的范围,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
9.已知两个不同的平面α,β和两条不重合的直线m,n,则下列命题正确的是( )
| A. | 若m∥n,n?α,则m∥α | B. | 若α⊥β,α∩β=n,m⊥n,则m⊥β | ||
| C. | 若m?α,n?α,m∥β,n∥β,则α∥β | D. | 若m⊥β,m?α,则α⊥β |
10.直线l:x-2y+2=0过椭圆的上焦点F1和一个顶点B,该椭圆的离心率为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
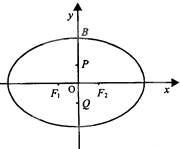 如图:设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右两个焦点分别为F1,F2,短轴的上端点为B,短轴上的两个三等分点为P,Q,且F1PF2Q为正方形,若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$,则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$.
如图:设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右两个焦点分别为F1,F2,短轴的上端点为B,短轴上的两个三等分点为P,Q,且F1PF2Q为正方形,若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$,则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$. 如图把椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的长轴AB分成8分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…P7七个点,F是椭圆的一个焦点,则|P1F|+|P2F|+…+|P7F|=28.
如图把椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的长轴AB分成8分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…P7七个点,F是椭圆的一个焦点,则|P1F|+|P2F|+…+|P7F|=28.