题目内容
19．
已知A（2，4），B（1，1），C（4，2）．给出平面区域为三角形ABC的内部及其边界，若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a值等于（ ）| A． | $\frac{1}{3}$ | B． | 6 | C． | 3 | D． | 1 |
分析 作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合进行求解即可．
解答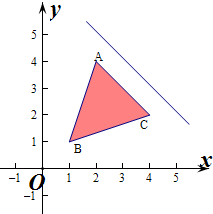 
解：由z=ax+y（a＞0）得y=-ax+z（a＞0）
直线y=-ax+z（a＞0）是斜率为-a，y轴上的截距为z的直线，
从题图可以看出，当-a等于直线AC的斜率时，
目标函数取得最大值的最优解有无穷多个，线段AC上的所有点都是最优解．
则-a=kAC=$\frac{4-2}{2-4}$=-1，
∴a=1，
故选：D．
点评 本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
9．已知两个不同的平面α，β和两条不重合的直线m，n，则下列命题正确的是（ ）
| A． | 若m∥n，n?α，则m∥α | B． | 若α⊥β，α∩β=n，m⊥n，则m⊥β | ||
| C． | 若m?α，n?α，m∥β，n∥β，则α∥β | D． | 若m⊥β，m?α，则α⊥β |
10．直线l：x-2y+2=0过椭圆的上焦点F1和一个顶点B，该椭圆的离心率为（ ）
| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{2}{5}$ |
7．
某校高三年级100名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100]，这100名学生数学成绩在[70，100]分数段内的人数为（ ）
某校高三年级100名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100]，这100名学生数学成绩在[70，100]分数段内的人数为（ ）| A． | 60 | B． | 55 | C． | 50 | D． | 45 |
14．下列各组中的两个函数是同一函数的是（ ）
| A． | f（x）=$\frac{{x}^{2}-1}{x-1}$和f（x）=x+1 | |
| B． | f（r）=πr2（r≥0）和g（x）=πx2（x≥0） | |
| C． | f（x）=logaax（a＞0且a≠1）和g（x）=${a}^{lo{g}_{a}x}$（a＞0且a≠1） | |
| D． | f（x）=x和g（t）和g（t）=$\sqrt{{t}^{2}}$ |
如图ABCD为正方形，VD⊥平面ABCD，VD=AD=2，F为VA中点，E为CD中点．
9．若集合A={x|log${\;}_{\sqrt{2}}$x＜2}，B={x|x-1|≤2}，则（CRA）∩B=（ ）
| A． | [-1，0]∪[2，3] | B． | （-1，0）∪（2，3） | C． | [2，3] | D． | （2，3] |