题目内容
(本小题满分12分)
设a∈R,函数f(x)= e -x(ax2 + a + 1),其中e是自然对数的底数;
(1)求函数f(x)的单调区间;
(2)当 -1<a<0 时,求函数f(x)在 [ 1,2 ] 上的最小值。
设a∈R,函数f(x)= e -x(ax2 + a + 1),其中e是自然对数的底数;
(1)求函数f(x)的单调区间;
(2)当 -1<a<0 时,求函数f(x)在 [ 1,2 ] 上的最小值。
(1)由已知:f′(x)=-e-x(ax2+a+1)+ e-x·2ax=e-x(-ax2+2ax-a-1)。
因为e-x>0,只需讨论g(x)=-ax2+2ax-a-1值的情况;
当a=0时,g(x)=-1<0,即f′(x)<0,
所以f(x)在R上是减函数;
当a>0时,g(x)=0的△=4a2-4(a2+a)=-4a<0,所以g(x)<0,即f′(x)<0,
所以f(x)在R上是减函数; (4分)
当a<0时,g(x)=0有两根,且<。
所以,在区间(-∞,)上,g(x)>0,即f′(x)>0,f(x)在此区间上是增函数,
在区间(,)上,g(x)<0,即f′(x)<0,f(x)在此区间上是减函数,
在区间(,+∞)上,g(x)>0,即f′(x)>0,f(x)在此区间上是增函数。
综上所述,当a≥0时,f(x)的单调减区间为(-∞,+∞),
当a<0时,f(x)的单调增区间为(-∞,)和(,+∞),
f(x)的单调减区间为(,)。(8分)
(2)当-1<a<0时,<1,>2,所以,在[1,2]上,f(x)单调递减,
所以f(x)在[1,2]上的最小值为f(2)=。(12分)
因为e-x>0,只需讨论g(x)=-ax2+2ax-a-1值的情况;
当a=0时,g(x)=-1<0,即f′(x)<0,
所以f(x)在R上是减函数;
当a>0时,g(x)=0的△=4a2-4(a2+a)=-4a<0,所以g(x)<0,即f′(x)<0,
所以f(x)在R上是减函数; (4分)
当a<0时,g(x)=0有两根,且<。
所以,在区间(-∞,)上,g(x)>0,即f′(x)>0,f(x)在此区间上是增函数,
在区间(,)上,g(x)<0,即f′(x)<0,f(x)在此区间上是减函数,
在区间(,+∞)上,g(x)>0,即f′(x)>0,f(x)在此区间上是增函数。
综上所述,当a≥0时,f(x)的单调减区间为(-∞,+∞),
当a<0时,f(x)的单调增区间为(-∞,)和(,+∞),
f(x)的单调减区间为(,)。(8分)
(2)当-1<a<0时,<1,>2,所以,在[1,2]上,f(x)单调递减,
所以f(x)在[1,2]上的最小值为f(2)=。(12分)
略

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
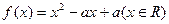 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在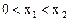 , 使得不等式
, 使得不等式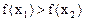 成立. 若
成立. 若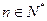 ,
,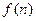 是数列
是数列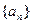 的前
的前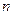 项和.
项和.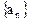 的通项公式;
的通项公式;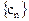 中,所有满足
中,所有满足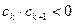 的正整数
的正整数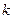 的个数称为这个数列
的个数称为这个数列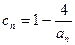 (n为正整数),求数列
(n为正整数),求数列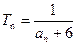 (
(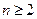 且
且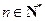 ),使不等式
),使不等式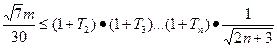 恒成立,求正整数
恒成立,求正整数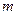 的最大值
的最大值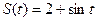 ,则它的初始速度是 ( )
,则它的初始速度是 ( )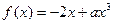 ,若
,若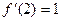 ,则
,则 ( )
( )
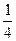
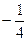
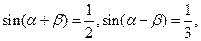 则
则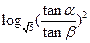 等于 ( )
等于 ( ) 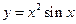 ,则
,则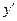 =
=  ,则函数
,则函数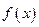 在
在 处的导数
处的导数