题目内容
已知函数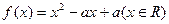 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在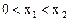 , 使得不等式
, 使得不等式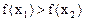 成立. 若
成立. 若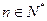 ,
,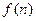 是数列
是数列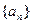 的前
的前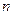 项和.
项和.
(I)求数列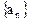 的通项公式;
的通项公式;
(II)设各项均不为零的数列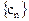 中,所有满足
中,所有满足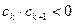 的正整数
的正整数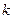 的个数称为这个数列
的个数称为这个数列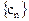 的变号数,令
的变号数,令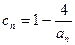 (n为正整数),求数列
(n为正整数),求数列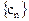 的变号数;
的变号数;
(Ⅲ)设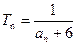 (
(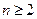 且
且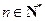 ),使不等式
),使不等式
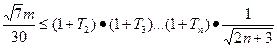 恒成立,求正整数
恒成立,求正整数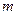 的最大值
的最大值
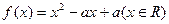 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在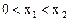 , 使得不等式
, 使得不等式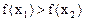 成立. 若
成立. 若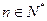 ,
,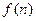 是数列
是数列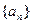 的前
的前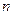 项和.
项和.(I)求数列
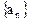 的通项公式;
的通项公式;(II)设各项均不为零的数列
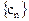 中,所有满足
中,所有满足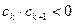 的正整数
的正整数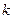 的个数称为这个数列
的个数称为这个数列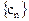 的变号数,令
的变号数,令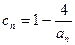 (n为正整数),求数列
(n为正整数),求数列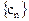 的变号数;
的变号数;(Ⅲ)设
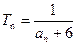 (
(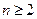 且
且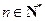 ),使不等式
),使不等式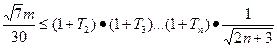 恒成立,求正整数
恒成立,求正整数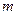 的最大值
的最大值解:(I)∵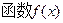 在定义域内有且只有一个零点
在定义域内有且只有一个零点
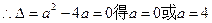 ……1分
……1分
当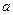 =0时,函数
=0时,函数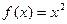 在
在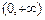 上递增 故不存在
上递增 故不存在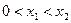 ,
,
使得不等式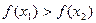 成立 …… 2分
成立 …… 2分
综上,得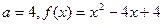 …….3分
…….3分
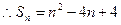
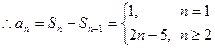 …………4分
…………4分
(II)解法一:由题设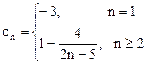
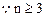 时,
时,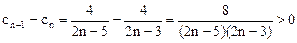
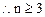 时,数列
时,数列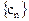 递增
递增 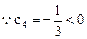
由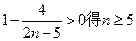 可知
可知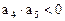
即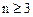 时,有且只有1个变号数; 又
时,有且只有1个变号数; 又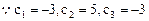
即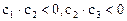 ∴此处变号数有2个
∴此处变号数有2个
综上得数列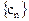 共有3个变号数,即变号数为3 ……9分
共有3个变号数,即变号数为3 ……9分
解法二:由题设
当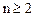 时,令
时,令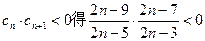
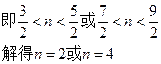
又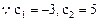
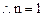 时也有
时也有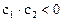
综上得数列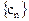 共有3个变号数,即变号数为3 …………9分
共有3个变号数,即变号数为3 …………9分
(Ⅲ)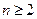 且
且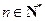 时,
时,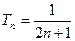
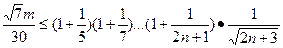
可转化为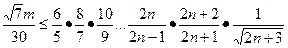 .
.
设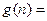
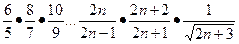 ,
,
则当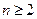 且
且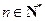 ,
,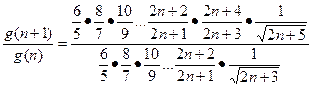
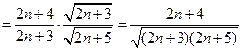
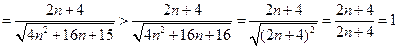 .
.
所以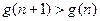 ,即当
,即当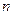 增大时,
增大时,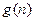 也增大.
也增大.
要使不等式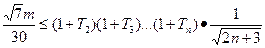 对于任意的
对于任意的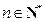 恒成立,
恒成立,
只需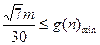 即可.因为
即可.因为 ,
,
所以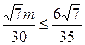 . 即
. 即 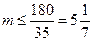
所以,正整数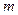 的最大值为5. ……………13分
的最大值为5. ……………13分
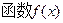 在定义域内有且只有一个零点
在定义域内有且只有一个零点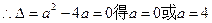 ……1分
……1分当
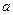 =0时,函数
=0时,函数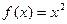 在
在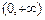 上递增 故不存在
上递增 故不存在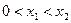 ,
,使得不等式
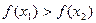 成立 …… 2分
成立 …… 2分综上,得
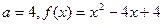 …….3分
…….3分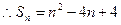
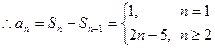 …………4分
…………4分 (II)解法一:由题设
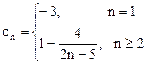
 时,
时,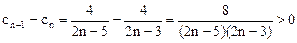
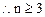 时,数列
时,数列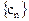 递增
递增 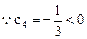
由
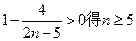 可知
可知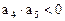
即
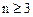 时,有且只有1个变号数; 又
时,有且只有1个变号数; 又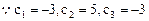
即
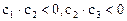 ∴此处变号数有2个
∴此处变号数有2个综上得数列
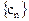 共有3个变号数,即变号数为3 ……9分
共有3个变号数,即变号数为3 ……9分 解法二:由题设

当
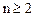 时,令
时,令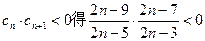
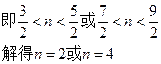
又
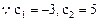
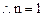 时也有
时也有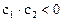
综上得数列
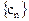 共有3个变号数,即变号数为3 …………9分
共有3个变号数,即变号数为3 …………9分(Ⅲ)
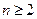 且
且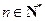 时,
时,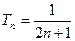
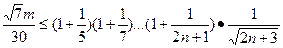
可转化为
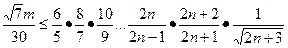 .
.设
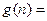
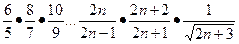 ,
,则当
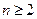 且
且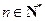 ,
,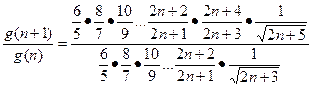
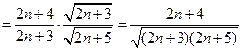
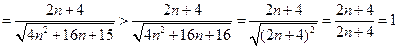 .
.所以
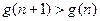 ,即当
,即当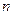 增大时,
增大时,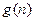 也增大.
也增大.要使不等式
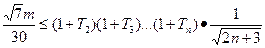 对于任意的
对于任意的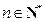 恒成立,
恒成立,只需
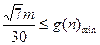 即可.因为
即可.因为 ,
,所以
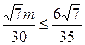 . 即
. 即 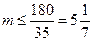
所以,正整数
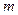 的最大值为5. ……………13分
的最大值为5. ……………13分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
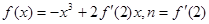 ,则二项式
,则二项式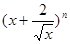 展开式中常数
展开式中常数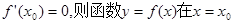 取得极值;
取得极值;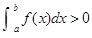 ,则f(x)>0在
,则f(x)>0在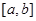 上恒成立;
上恒成立;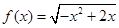 ,则
,则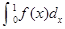 的值为
的值为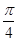 ;
;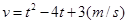 运动,从时刻
运动,从时刻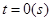 到
到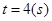 时质点运动的路程为
时质点运动的路程为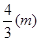 。
。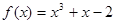 在
在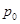 处的切线平行于直线
处的切线平行于直线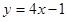 ,则
,则
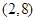

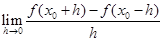 =( )
=( )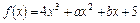 的图象在
的图象在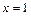 处的切线方程为
处的切线方程为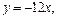
 求函
求函 数
数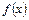 的解析式;
的解析式;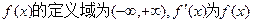 的导函数,函数
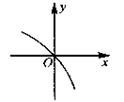
的导函数,函数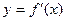 的图象如图所示,且
的图象如图所示,且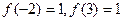 ,则不等式
,则不等式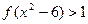 的
的 解集为( **
解集为( ** *)
*)
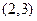
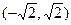
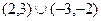
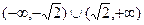
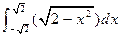 = 。
= 。