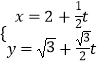题目内容
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
【答案】
(1)解:将圆C的方程x2+y2﹣8y+12=0配方得标准方程为x2+(y﹣4)2=4,
则此圆的圆心为(0,4),半径为2.若直线l与圆C相切,则有 ![]() .解得
.解得 ![]() .
.
(2)解:联立方程 ![]() 并消去y,
并消去y,
得(a2+1)x2+4(a2+2a)x+4(a2+4a+3)=0.
设此方程的两根分别为x1、x2,
所以x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
则AB= ![]() =
= ![]() =2
=2 ![]()
两边平方并代入解得:a=﹣7或a=﹣1,
∴直线l的方程是7x﹣y+14=0和x﹣y+2=0.
另解:圆心到直线的距离为d= ![]() ,
,
AB=2 ![]() =2
=2 ![]() ,可得d=
,可得d= ![]() ,
,
解方程可得a=﹣7或a=﹣1,
∴直线l的方程是7x﹣y+14=0和x﹣y+2=0.
【解析】把圆的方程化为标准方程后,找出圆心坐标与圆的半径r,(1)当直线l与圆相切时,圆心到直线的距离d等于圆的半径r,利用点到直线的距离公式表示出圆心到直线l的距离d,让d等于圆的半径r,列出关于a的方程,求出方程的解即可得到a的值;(2)联立圆C和直线l的方程,消去y后,得到关于x的一元二次方程,然后利用韦达定理表示出AB的长度,列出关于a的方程,求出方程的解即可得到a的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目