题目内容
【题目】在平面直角坐标系xOy中,直线l的参数方程为 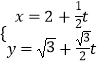 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2.
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C1交于A、B两点,求|MA|+|MB|的值.
),直线l与曲线C1交于A、B两点,求|MA|+|MB|的值.
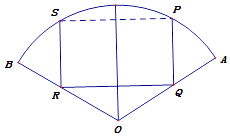
(2)设曲线C1经过伸缩变换 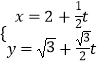 得到曲线C2 , 求曲线C2的内接矩形周长的最大值.
得到曲线C2 , 求曲线C2的内接矩形周长的最大值.
【答案】
(1)解:曲线C的极坐标方程为ρ=2,则曲线C的直角坐标方程为:x2+y2=4,
直线l: 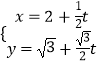 ,转化成普通方程为:y﹣
,转化成普通方程为:y﹣ ![]() x+
x+ ![]() =0,
=0,
设A,B两点对应的参数分别为t1,t2,
将直线l的参数方程带入圆的直角坐标方程x2+y2=4,
整理得:t2+5t+3=0,
△>0,故t1,t2是方程的两个根,
∴t1+t2=﹣5,t1t2=3,
|MA|+|MB|=|t1|+|t2|=|t1+t2|=5;
(2)解: 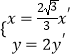 代入曲线C的方程得:
代入曲线C的方程得: ![]() ,
,
设曲线C′的内接矩形周长为P,
曲线C′的内接矩形的第一象限内的顶点为N(x′,y′)(0<x< ![]() ,0<y<1),
,0<y<1),
x′2+3y′2=3,x′= ![]() ,
,
P=4x′+4y′=4 ![]() +4y′,
+4y′,
令f(y)=4 ![]() +4y′,
+4y′,
f′(y)= ![]() +4,
+4,
令f′(y′)=0得y= ![]() ,
,
当0<y′< ![]() 时,f′(y′)>0,当
时,f′(y′)>0,当 ![]() <y<1时,f′(y′)<0.
<y<1时,f′(y′)<0.
∴当y′= ![]() 时,f(y)取得最大8.
时,f(y)取得最大8.
曲线C′的内接矩形周长的最大8
【解析】(1)求得曲线C的直角坐标方程,把直线l代入圆的直角坐标方程,化简后利用韦达定理可求t1+t2 , t1t2的值,由|MA|+|MB|=|t1﹣t2|= ![]() ,即可求得|MA|+|MB|的值;(2)设矩形的顶点坐标为(x′,y′),则根据x′,y′的关系消元得出P关于x(或y)的函数,利用导数,求出此函数的最大值.
,即可求得|MA|+|MB|的值;(2)设矩形的顶点坐标为(x′,y′),则根据x′,y′的关系消元得出P关于x(或y)的函数,利用导数,求出此函数的最大值.

【题目】已知某产品的历史收益率的频率分布直方图如图所示.
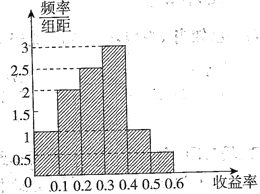
(1)试估计该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从表中五组销量数据中随机抽取两组,记其中销量超过6万份的组数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
【题目】某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位女教师的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |