Question

【题目】已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若a，b∈[﹣1，1]，a+b≠0时，有 ＞0成立． （Ⅰ）判断f（x）在[﹣1，1]上的单调性，并证明；
（Ⅱ）解不等式：f（2x﹣1）＜f（1﹣3x）；
（Ⅲ）若f（x）≤m2﹣2am+1对所有的a∈[﹣1，1]恒成立，求实数m的取值范围．

Answer 1

【答案】解：（Ⅰ）任取x1 ， x2∈[﹣1，1]，且x1＜x2 ， 则﹣x2∈[﹣1，1]，∵f（x）为奇函数， ∴f（x1）﹣f（x2）=f（x1）+f（﹣x2）= （x1﹣x2），…（2分）
由已知得 ＞0，x1﹣x2＜0，∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2）．
∴f（x）在[﹣1，1]上单调递增．
（Ⅱ）∵f（x）在[﹣1，1]上单调递增，∴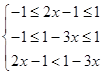
∴不等式的解集为 ．
（Ⅲ）∵f（1）=1，f（x）在[﹣1，1]上单调递增．∴在[﹣1，1]上，f（x）≤1．
问题转化为m2﹣2am+1≥1，即m2﹣2am≥0，对a∈[﹣1，1]恒成立．
下面来求m的取值范围．设g（a）=﹣2ma+m2≥0．
①若m=0，则g（a）=0≥0，对a∈[﹣1，1]恒成立．
②若m≠0，则g（a）为a的一次函数，若g（a）≥0，对a∈[﹣1，1]恒成立，
必须g（﹣1）≥0且g（1）≥0，∴m≤﹣2或m≥2．
综上，m=0 或m≤﹣2或m≥2
【解析】（Ⅰ）任取x1 ， x2∈[﹣1，1]，且x1＜x2 ， 利用函数的单调性的定义证明f（x）在[﹣1，1]上单调递增．（Ⅱ）利用f（x）在[﹣1，1]上单调递增，列出不等式组，即可求出不等式的解集．（Ⅲ）问题转化为m2﹣2am≥0，对a∈[﹣1，1]恒成立，通过①若m=0，②若m≠0，分类讨论，判断求解即可．