题目内容
椭圆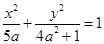
的焦点在
轴上，则它的离心率的取值范围为（ ）
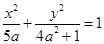的焦点在轴上，则它的离心率的取值范围为（ ）A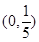． | B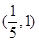． | C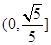． | D． |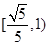
C
此题考查椭圆的标准方程的形式、离心率的计算、椭圆中离心率的范围；由已知得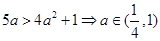
，且
，所以选C；此题利用均值不等式求的范围；
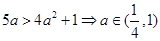，且，所以选C；此题利用均值不等式求的范围；
练习册系列答案
相关题目
题目内容
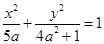的焦点在轴上，则它的离心率的取值范围为（ ）| A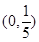． | B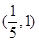． | C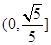． | D． |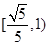
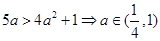，且，所以选C；此题利用均值不等式求的范围；
有公共焦点，且离心率
的双曲线的方程是
的离心率为
，一个焦点为
．
的方程；
交椭圆
，
两点，若点
为圆心的圆上，求
的值．
的右顶点是
，上下两个顶点分别为
，四边形
是矩形（
为原点），点
分别为线段
的中点．
与直线
的交点在椭圆
上；
的直线交椭圆于
两点，
为
关于
轴的对称点（
不共线），问：直线
是否经过
的离心率为
，以原点为圆心，椭圆短半轴长为半径的圆与直线
相切，
分别是椭圆的左右两个顶点， 
为椭圆
上的动点.
与
的斜率分别为
，证明：
为定值；
为过
轴的直线上的点，若
，求点
与双曲线
有相同的焦点
、
，点
是
是一个以
为底的等腰三角形，
,
,则
＋
＝1
的左．右焦点为
，离心率为
，直线
与x轴、y轴分别交于点
，
是直线
与椭圆C的一个公共点，
是点
关于直线
＝
； （Ⅱ）确定
的值，使得
是等腰三角形.
的一个焦点坐标为(0,1)，则实数
的值等于_____ ____,
的准线与x轴交于F1，焦点为F2；以F1,F2为焦点，离心率
的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q，M是抛物线上一动点，且M在P与Q之间运动.
的边长恰好是三个连续的自然数时，求
面积的最大值.