题目内容
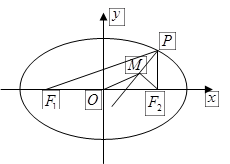
如图椭圆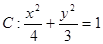 的右顶点是
的右顶点是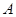 ,上下两个顶点分别为
,上下两个顶点分别为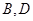 ,四边形
,四边形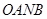 是矩形(
是矩形(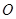 为原点),点
为原点),点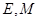 分别为线段
分别为线段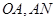 的中点.
的中点.
(Ⅰ)证明:直线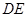 与直线
与直线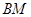 的交点在椭圆
的交点在椭圆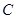 上;
上;
(Ⅱ)若过点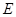 的直线交椭圆于
的直线交椭圆于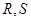 两点,
两点,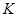 为
为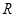 关于
关于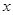 轴的对称点(
轴的对称点(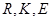 不共线),问:直线
不共线),问:直线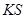 是否经过
是否经过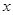 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.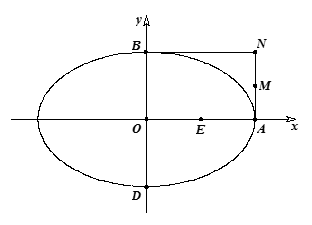
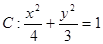 的右顶点是
的右顶点是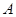 ,上下两个顶点分别为
,上下两个顶点分别为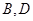 ,四边形
,四边形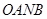 是矩形(
是矩形(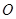 为原点),点
为原点),点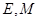 分别为线段
分别为线段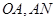 的中点.
的中点.(Ⅰ)证明:直线
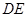 与直线
与直线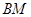 的交点在椭圆
的交点在椭圆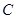 上;
上;(Ⅱ)若过点
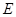 的直线交椭圆于
的直线交椭圆于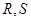 两点,
两点,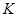 为
为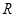 关于
关于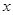 轴的对称点(
轴的对称点(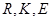 不共线),问:直线
不共线),问:直线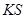 是否经过
是否经过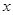 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
(1)由题意,得 ,
,
所以直线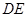 的方程
的方程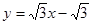 ,直线
,直线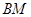 的方程为
的方程为 ,------2分
,------2分
由 ,得
,得 ,
,
所以直线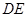 与直线
与直线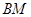 的交点坐标为
的交点坐标为 ,---------------4分
,---------------4分
因为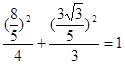 ,所以点
,所以点 在椭圆
在椭圆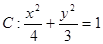 上.---------6分
上.---------6分
(2)设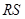 的方程为
的方程为 ,代入
,代入 ,
,
得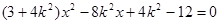 ,
,
设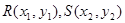 ,则
,则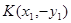 ,
,
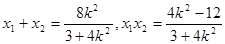 ,
,
直线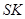 的方程为
的方程为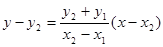 ,
,
令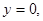 得
得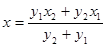 ,
,
将 ,
, 代入上式得
代入上式得
(9设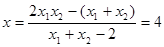 ,
,
所以直线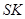 经过
经过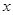 轴上的点
轴上的点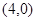 .
.
 ,
,所以直线
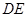 的方程
的方程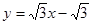 ,直线
,直线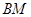 的方程为
的方程为 ,------2分
,------2分由
 ,得
,得 ,
,所以直线
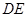 与直线
与直线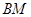 的交点坐标为
的交点坐标为 ,---------------4分
,---------------4分因为
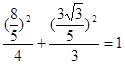 ,所以点
,所以点 在椭圆
在椭圆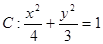 上.---------6分
上.---------6分(2)设
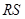 的方程为
的方程为 ,代入
,代入 ,
,得
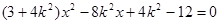 ,
,设
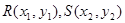 ,则
,则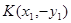 ,
,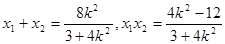 ,
,直线
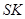 的方程为
的方程为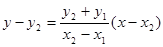 ,
,令
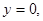 得
得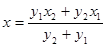 ,
,将
 ,
, 代入上式得
代入上式得(9设
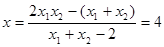 ,
,所以直线
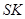 经过
经过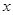 轴上的点
轴上的点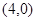 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
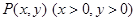 是双曲线
是双曲线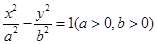 上的动点,
上的动点,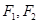 是双曲线的焦点,
是双曲线的焦点,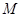 是
是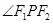 的平分线上一点,且
的平分线上一点,且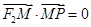 .某同学用以下方法研究
.某同学用以下方法研究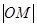 :延长
:延长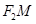 交
交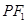 于点
于点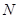 ,可知
,可知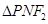 为等腰三角形,且
为等腰三角形,且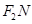 的中点,得
的中点,得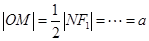 .类似地:点
.类似地:点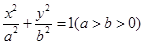 上的动点,
上的动点,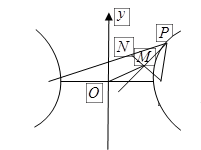
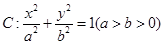 的离心率为
的离心率为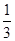 ,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线
,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线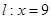 于G点,直线MB交直线
于G点,直线MB交直线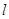 于H点。
于H点。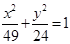 共焦点,且以
共焦点,且以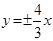 为渐近线,求双曲线方程.
为渐近线,求双曲线方程.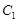 :
: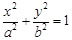 (
(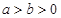 )的离心率为
)的离心率为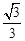 ,直线
,直线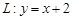 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆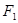 ,右焦点为
,右焦点为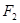 ,直线
,直线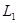 过点
过点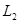 垂直
垂直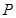 ,线段
,线段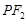 的垂直平分线交
的垂直平分线交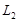 于点
于点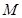 .
.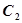 的方程;
的方程;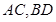 为点
为点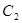 的过点
的过点 面积的最小值.
面积的最小值.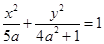 的焦点在
的焦点在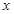 轴上,则它的离心率的取值范围为( )
轴上,则它的离心率的取值范围为( )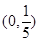
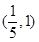
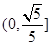
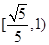
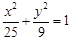 ,F是右焦点,
,F是右焦点,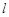 是过点F的一条直线(不与
是过点F的一条直线(不与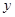 轴平行),交椭圆于A、B两点,
轴平行),交椭圆于A、B两点, 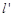 是AB的中垂线,交椭圆的长轴于一点D,则
是AB的中垂线,交椭圆的长轴于一点D,则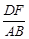 的值是 .
的值是 .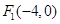 ,
,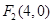 ,P在椭圆上,若 △
,P在椭圆上,若 △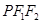 的面积的最大值为12,则椭圆方程为
的面积的最大值为12,则椭圆方程为



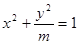 的下焦点为
的下焦点为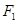 、上焦点为
、上焦点为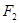 ,其离心 率
,其离心 率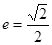 。过焦点F2且与
。过焦点F2且与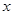 轴不垂直的直线l交椭圆于A、B两点。
轴不垂直的直线l交椭圆于A、B两点。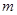 的值;
的值;