题目内容
【题目】为备战2016年奥运会,甲、乙两位射击选手进行了强化训练.现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5
(1)画出甲、乙两位选手成绩的茎叶图;
(2)现要从中选派一人参加奥运会封闭集训,从统计学角度,你认为派哪位选手参加合理?简单说明理由;
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为ξ,求ξ的分布列及均值E(ξ).
【答案】(1)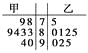
(2)选派甲合适
(3)ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴E(ξ)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.
【解析】
(1)甲、乙两位选手成绩的茎叶图如图:

(2)因为![]() 甲=
甲=![]() 乙=8.5,又
乙=8.5,又![]() =0.27,
=0.27,![]() =0.405,得
=0.405,得![]() <
<![]() ,所以选派甲合适.
,所以选派甲合适.
(3)依题意得,乙不低于8.5分的频率为![]() ,ξ的可能取值为0,1,2,3.则ξ~B
,ξ的可能取值为0,1,2,3.则ξ~B![]() ,
,
∴P(ξ=k)=![]()
![]() 3-k
3-k![]() k=
k=![]()
![]() 3,k=0,1,2,3.
3,k=0,1,2,3.
所以ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴E(ξ)=np=3×![]() =
=![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某班级体育课举行了一次“投篮比赛”活动,为了了解本次投篮比赛学生总体情况,从中抽取了甲乙两个小组样本分数的茎叶图如图所示.
5 | 6 | 5 | 8 | ||||||
6 | 0 | 1 | 3 | 6 | 2 | 4 | 6 | 9 | |
7 | 1 | 2 | 7 | 1 | 3 | ||||
8 | 0 | 1 | 8 | 1 | |||||
甲 | 乙 | ||||||||
(1)分别求甲乙两个小组成绩的平均数与方差;
(2)分析比较甲乙两个小组的成绩;
(3)从甲组高于70分的同学中,任意抽取2名同学,求恰好有一名同学的得分在[80,90)的概率.