题目内容
【题目】我校为丰富师生课余活动,计划在一块直角三角形![]() 的空地上修建一个占地面积为
的空地上修建一个占地面积为![]() (平方米)的
(平方米)的![]() 矩形健身场地,如图,点
矩形健身场地,如图,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 点在斜边
点在斜边![]() 上,已知
上,已知![]() ,
, ![]() 米,
米, ![]() 米,
米, ![]() .设矩形
.设矩形![]() 健身场地每平方米的造价为
健身场地每平方米的造价为![]() 元,再把矩形
元,再把矩形![]() 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为![]() 元(
元(![]() 为正常数)
为正常数)
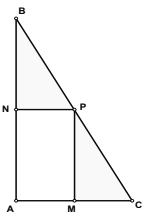
(1)试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)求总造价![]() 关于面积
关于面积![]() 的函数
的函数![]() ;
;
(3)如何选取![]() ,使总造价
,使总造价![]() 最低(不要求求出最低造价)
最低(不要求求出最低造价)
【答案】(1) ![]() (2) 选取
(2) 选取![]() 的长为12米或18米时总造价
的长为12米或18米时总造价![]() 最低
最低
【解析】试题分析:(1)在![]() 中,显然
中,显然![]() ,
,
![]() ,根据面积公式写出矩形面积;(2)矩形
,根据面积公式写出矩形面积;(2)矩形![]() 健身场地造价
健身场地造价![]() ,又
,又![]() 的面积为
的面积为![]() ,即草坪造价
,即草坪造价![]() ,写出总造价即可;(3)根据均值不等式
,写出总造价即可;(3)根据均值不等式![]() 即可求出造价的最小值.
即可求出造价的最小值.
试题解析:
(1)在![]() 中,显然
中,显然![]() ,
,
![]() ,
,
矩形![]() 的面积
的面积![]()
于是![]() 为所求
为所求
(2)矩形![]() 健身场地造价
健身场地造价![]()
又![]() 的面积为
的面积为![]() ,即草坪造价
,即草坪造价![]() ,
,
由总造价
(3) ![]()
当且仅当![]() 即
即![]() 时等号成立,此时,
时等号成立,此时, ![]() 解得
解得![]() 或
或![]()
答:选取![]() 的长为12米或18米时总造价
的长为12米或18米时总造价![]() 最低.
最低.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
【题目】某地![]() 户家庭的年收入
户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)的统计资料如下表:
(万元)的统计资料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留到小数点后
的线性回归方程;(结果保留到小数点后![]() 为数字)
为数字)
(2)利用(1)中的回归方程,分析这![]() 户家庭的年饮食支出的变化情况,并预测该地年收入
户家庭的年饮食支出的变化情况,并预测该地年收入![]() 万元的家庭的年饮食支出.(结果保留到小数点后
万元的家庭的年饮食支出.(结果保留到小数点后![]() 位数字)
位数字)
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
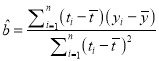 ,
, ![]()