题目内容
【题目】已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m∥α,n∥α,则 m∥n
B.若α⊥γ,β⊥γ,则α∥β
C.若m⊥α,n⊥β,且α⊥β,则m⊥n.
D.若m∥α,n∥α,且mβ, nβ,则α∥β
【答案】C
【解析】
平行于同一平面的两条直线可能平行、异面、相交,所以A错;
垂直于同一平面的两个平面可能平行,也可能相交,所以B错;
一个平面内两条相交直线平行于另一个平面才能判定面面平行,所以D错;
两个平面垂直,可得这两个平面的垂线互相垂直.
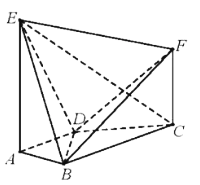
用具体例子辨析:长方体![]() 中,
中,![]() 是
是![]() 的中点,则
的中点,则![]()
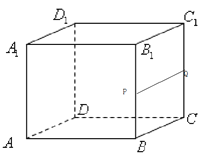
A选项:直线![]() 均与平面
均与平面![]() 平行,但
平行,但![]() 不平行,所以错误;
不平行,所以错误;
B选项:平面![]() 和平面
和平面![]() 均与平面
均与平面![]() 垂直,但平面
垂直,但平面![]() 和平面
和平面![]() 相交,不平行,所以错误;
相交,不平行,所以错误;
C选项:若m⊥α,n⊥β,且α⊥β,可以考虑直线m,n的方向向量是平面α,β的法向量,两平面垂直,则法向量垂直,即m⊥n,选项正确;
D选项:平面![]() 内的两条直线
内的两条直线![]() 均平行于
均平行于![]() 且不在平面
且不在平面![]() 内,即直线
内,即直线![]() 均平行于平面
均平行于平面![]() ,但平面
,但平面![]() 不平行于平面
不平行于平面![]() ,所以错误.
,所以错误.
故选:C

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目