Question

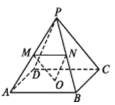
【题目】如图所示，在斜三棱柱中，底面是等腰三角形，，是的中点，侧面底面.

（1）求证：；

（2）过侧面的对角线的平面交侧棱于点，若，求证：截面侧面；

（3）若截面平面，成立吗？请说明理由.

Answer 1

【答案】（1）见解析； （2）见解析； （3）见解析.

【解析】

（1）根据面面垂直的性质证明侧面，即可证得；

（2）延长，与的延长线交于点N，证明侧面即可；

（3）过M作于点E，连接，根据面面垂直的性质，侧面，，结合长度关系即可得解.

（1）证明：，D是的中点，.

∵底面侧面，底面侧面，底面，

侧面.

又侧面，.

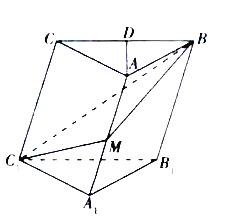
（2）证明：如图，延长，与的延长线交于点N，

连接，则平面，

，.，

，

，由已知侧面底面

所以侧面底面，交线为，

底面，

侧面，平面，

∴截面侧面.

（3）成立.理由如下：

过M作于点E，连接.

∵截面侧面，根据面面垂直的性质，

侧面.

又侧面，，

四点共面.

侧面，平面，

平面平面，.

∴四边形是平行四边形，

又，.

是的中点，，

.

.