题目内容
10.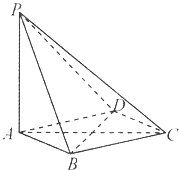 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与平面PAC所成角的余弦值;
(3)若PA=4,求平面PBC与平面PDC所成角的余弦值.
分析 (1)由BD⊥AC,BD⊥PA,根据直线与平面垂直的判定定理即可得证;
(2)令BD∩AC=O,连接PO,由(1)可得∠BPO即为PB与面PAC所成的角,利用cos∠BPO=$\frac{PO}{PB}$即可得解.
(3)如图,以O为原点,OB,OC所在直线分别为x轴,y轴建立空间直角坐标系,设平面PBC的法向量为$\overrightarrow{{n}_{1}}$,平面PCD的法向量为$\overrightarrow{{n}_{2}}$,由cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=|$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$|即可得解.
解答 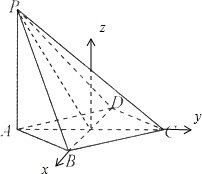 (本题12分)
(本题12分)
解:(1)证明:
$\begin{array}{l}BD⊥AC---------------1'\\ BD⊥PA---------------1'\\ PA∩AC=A---------------1'\\∴BD⊥面PAC\end{array}$
(2)解:
$\begin{array}{l}令BD∩AC=O,连PO---------------1'\\∠BPO即为PB与面PAC所成角---------------1'\\ cos∠BPO=\frac{{\sqrt{14}}}{4}---------------2'\end{array}$
(3)解:
$\begin{array}{l}建系:以O为原点,OB,OC所在直线分别为x轴,y轴建立空间直角坐标系---------------1'\\ 设面PBC的法向量\overrightarrow{n_1},面PDC的法向量\overrightarrow{n_2},\\ \overrightarrow{n_1}=(\sqrt{3},1,\frac{{\sqrt{3}}}{2})---------------1'\\ \overrightarrow{n_2}=(-\sqrt{3},1,\frac{{\sqrt{3}}}{2})---------------1'\\ cos<\overrightarrow{n_1},\overrightarrow{n_2}>=-\frac{5}{19}∵二面角所成角为锐角\\∴平面PBC与平面PDC所成角的余弦值为\frac{5}{19}---------------2'\end{array}$
点评 本题主要考查了直线与平面垂直的判定,二面角的平面角及求法,考查了空间想象能力和推理论证能力,考查了数形结合的思想和转化思想,属于基本知识的考查.
