题目内容
【题目】设函数![]() .
.
(1)当![]() 时,证明:
时,证明:![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(2)当![]() ,函数
,函数![]() 的零点个数,并说明理由;
的零点个数,并说明理由;
(3)求函数![]() 的对称中心,并说明理由.
的对称中心,并说明理由.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)化简函数![]() 的解析式,根据单调性的定义可证明出函数
的解析式,根据单调性的定义可证明出函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(2)判断函数![]() 在各区间
在各区间![]() 的单调性,从而得出结论;
的单调性,从而得出结论;
(3)将函数![]() 进行平移变换构造一个奇函数即可得出对称中心.
进行平移变换构造一个奇函数即可得出对称中心.
(1)当![]() 时,
时,![]() ,
,
任取![]() 、
、![]() 且
且![]() ,即
,即![]() ,
,
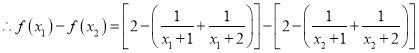
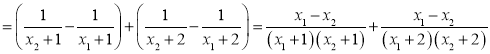 ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,
,
因此,函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
(2)当![]() 时,
时,![]() ,
,
显然当![]() 时,函数
时,函数![]() 为增函数,其中
为增函数,其中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以,函数![]() 在区间
在区间![]() 上有且只有一个零点;
上有且只有一个零点;
又当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以,函数![]() 在
在![]() 和
和![]() 上没有零点,
上没有零点,
因此,函数![]() 共有
共有![]() 个零点;
个零点;
(3)![]() ,
,
构造函数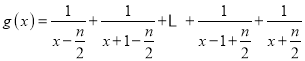 ,
,
可知,函数![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,
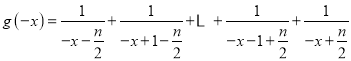
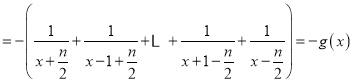 ,
,
所以,函数![]() 为奇函数,其对称中心为坐标原点,
为奇函数,其对称中心为坐标原点,
且有![]() ,
,
为了得到函数![]() 的图象,可将函数
的图象,可将函数![]() 的图象向上平移
的图象向上平移![]() 个单位长度,向左平移
个单位长度,向左平移![]() 个单位长度即可.
个单位长度即可.
因此,函数![]() 图象的对称中心坐标为
图象的对称中心坐标为![]() .
.

【题目】2019年1月1日新修订的个税法正式实施,规定:公民全月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算(预扣):
全月应缴纳所得额 | 税率 |
不超过3000元的部分 |
|
超过3000元至12000元的部分 |
|
超过12000元至25000元的部分 |
|
国家在实施新个税时,考虑到纳税人的实际情况,实施了《个人所得税税前专项附加扣税暂行办法》,具体如下表:
项目 | 每月税前抵扣金额(元) | 说明 |
子女教育 | 1000 | 一年按12月计算,可扣12000元 |
继续教育 | 400 | 一年可扣除4800元,若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元 |
大病医疗 | 5000 | 一年最高抵扣金额为60000元 |
住房贷款利息 | 1000 | 一年可扣除12000元,若夫妻双方在同一城市工作,可以选择一方来扣除 |
住房租金 | 1500/1000/800 | 扣除金额需要根据城市而定 |
赡养老人 | 2000 | 一年可扣除24000元,若不是独生子女,子女平均扣除.赡养老人年龄需要在60周岁及以上 |
老李本人为独生子女,家里有70岁的老人需要赡养,有一个女儿正读高三,他每月还需缴纳住房贷款2734元.若2019年11月老李工资,薪金所得为20000元,按照《个人所得税税前专项附加扣税暂行办法》,则老李应缴纳税款(预扣)为______元.
【题目】某租车公司给出的财务报表如下:
年度 项目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接单量(单) | 14463272 | 40125125 | 60331996 |
油费(元) | 214301962 | 581305364 | 653214963 |
平均每单油费 | 14.82 | 14.49 | |
平均每单里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为![]() .
.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里).