题目内容
设定点M(3, )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为 ,P到抛物线准线l的距为
,P到抛物线准线l的距为 ,则
,则 +
+ 取最小值时,P点的坐标为
取最小值时,P点的坐标为
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
C
解析试题分析:先判断出M(3, )在抛物线
)在抛物线 =2x的外部然后做出图形(如下图)则PM=d1过p作PN⊥直线x=
=2x的外部然后做出图形(如下图)则PM=d1过p作PN⊥直线x= 则PN=d2,根据抛物线的定义可得d1+d2=PM+PF故要使
则PN=d2,根据抛物线的定义可得d1+d2=PM+PF故要使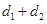 取最小值则只有当P,M,F三点共线时成立因此可求出MF所在的直线方程然后与抛物线的方程联立即可求出P点的坐标.
取最小值则只有当P,M,F三点共线时成立因此可求出MF所在的直线方程然后与抛物线的方程联立即可求出P点的坐标.
∵(3,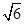 )在抛物线
)在抛物线 =2x上且
=2x上且 >
>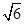 ∴M(3,
∴M(3, )在抛物线
)在抛物线 =2x的外部,∵抛物线y2=2x的焦点F(
=2x的外部,∵抛物线y2=2x的焦点F( ,0),准线方程为x=-
,0),准线方程为x=- ∴在抛物线
∴在抛物线 =2x上任取点P过p作PN⊥直线x=
=2x上任取点P过p作PN⊥直线x= 则PN=
则PN=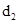
∴根据抛物线的定义可得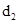 =PF,∴
=PF,∴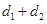 =PM+PF,∵PM+PF
=PM+PF,∵PM+PF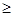 MF,∴当P,M,F三点共线时d1+d2取最小值,此时MF所在的直线方程为y-
MF,∴当P,M,F三点共线时d1+d2取最小值,此时MF所在的直线方程为y- =
= (x-3)即4x-3y-2=0,令4x-3y-2=0,
(x-3)即4x-3y-2=0,令4x-3y-2=0, =2x,联立方程组得到 x-=2,y=2,即当点的坐标为(2,2)时,
=2x,联立方程组得到 x-=2,y=2,即当点的坐标为(2,2)时,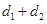 取最小值,故选C
取最小值,故选C
考点:抛物线的性质
点评:本题主要考察抛物线的性质,属常考题,较难.解题的关键是将d1+d2=PM+PN根据抛物线的定义转化为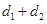 =PM+PF.
=PM+PF.

练习册系列答案
相关题目
已知 为双曲线C:
为双曲线C: 的左、右焦点,点
的左、右焦点,点 在
在 上,
上, ,则P到
,则P到 轴的距离为 ( )
轴的距离为 ( )
A. | B. | C. | D. |
如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A. | B. | C. | D.非上述结论 |
已知 是以
是以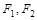 为焦点的椭圆
为焦点的椭圆 上的一点,若
上的一点,若
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. | B. | C. | D. |
 的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B.C,且
的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B.C,且 ,则双曲线M的离心率是( )
,则双曲线M的离心率是( ) B.
B.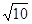 C.
C. D.
D.
 +
+ =1(a
=1(a b
b +
+ =1(a
=1(a ,则椭圆的离心率为( )
,则椭圆的离心率为( ) B.
B. C.
C.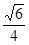 D.
D.
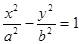 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x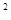 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ). 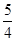
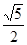
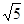
 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为( )
,则它的渐近线方程为( )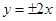
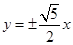
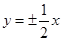
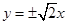
 的左焦点
的左焦点 引圆
引圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于
交双曲线右支于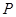 点,若
点,若 为线段
为线段 的中点,
的中点, 为坐标原点,则
为坐标原点,则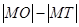 与
与 的大小关系为 ( )
的大小关系为 ( )