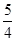题目内容
过双曲线 的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B.C,且
的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B.C,且 ,则双曲线M的离心率是( )
,则双曲线M的离心率是( )
A. B.
B.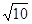 C.
C. D.
D.
C
解析试题分析:由双曲线方程可知,顶点A(1,0),所以直线l的方程为 ,分别与渐近线
,分别与渐近线 联立可得点B的横坐标为
联立可得点B的横坐标为 ,点C的横坐标为
,点C的横坐标为 ,因为
,因为 ,根据向量的坐标运算,可得
,根据向量的坐标运算,可得 ,所以双曲线的离心率为
,所以双曲线的离心率为 .
.
考点:本小题主要考查双曲线的基本性质和向量的坐标运算.
点评:解决本小题的关键是根据已知条件求出B,C的坐标,其实只求出横坐标即可,解决此类问题,要注意恰当转化.

练习册系列答案
相关题目
已知焦点在 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )
A.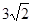 | B. | C. | D. |
已知平面上两点M(-5,0)和N(5,0),若直线上存在点P使|PM|-|PN|=6,则称该直线为“单曲型直线”,下列直线中是“单曲型直线”的是( )
① ; ②y=2; ③
; ②y=2; ③ ; ④
; ④ .
.
| A.①③ | B.③④ | C.②③ | D.①② |
椭圆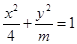 的焦距为2,则
的焦距为2,则 的值为( )
的值为( )
| A.3 | B. | C.3或5 | D.3或 |
设定点M(3, )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为 ,P到抛物线准线l的距为
,P到抛物线准线l的距为 ,则
,则 +
+ 取最小值时,P点的坐标为
取最小值时,P点的坐标为
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若△
两点,若△ 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )



 的一条渐近线与圆
的一条渐近线与圆 有公共点,则双曲线的离心率的取值范围是( )
有公共点,则双曲线的离心率的取值范围是( )



 :抛物线
:抛物线 的准线方程为
的准线方程为 ;命题
;命题 :平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )
:平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )



 ,
, 分别是双曲线
分别是双曲线 (
(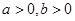 )的左右焦点,P为双曲线右支上一点,且满足
)的左右焦点,P为双曲线右支上一点,且满足 ,若直线
,若直线 与圆
与圆 相切,则双曲线的离心率e的值为
相切,则双曲线的离心率e的值为