题目内容
在阳光下将一个球放在水平面上,球的影子伸到距球与地面接触点 处,同一时刻,一个长
处,同一时刻,一个长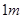 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为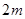 ,则该球的半径等于( )
,则该球的半径等于( )
 处,同一时刻,一个长
处,同一时刻,一个长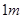 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为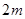 ,则该球的半径等于( )
,则该球的半径等于( )A.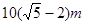 | B. | C.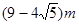 | D.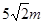 |
A
解:求所照影子的最远点,距离球的着地点10米,
过这个点有圆的两条切线,
根据一根长1米一端接触地面且与地面垂直的竹竿的影子长为2米知,光线与地面所成的角的正切是1 2∴球心与最远点的连线把角分成两部分,两个角相等,设为θ,则有1/ 2 =2tanθ /(1-tan2θ) ,
∴tanθ=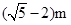 ,在直角三角形中,根据三角函数的定义得到球的半径是r,∴r /10 =
,在直角三角形中,根据三角函数的定义得到球的半径是r,∴r /10 =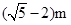 ,∴r=10
,∴r=10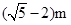 ,故半径为
,故半径为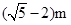 ,故选A.
,故选A.
过这个点有圆的两条切线,
根据一根长1米一端接触地面且与地面垂直的竹竿的影子长为2米知,光线与地面所成的角的正切是1 2∴球心与最远点的连线把角分成两部分,两个角相等,设为θ,则有1/ 2 =2tanθ /(1-tan2θ) ,
∴tanθ=
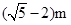 ,在直角三角形中,根据三角函数的定义得到球的半径是r,∴r /10 =
,在直角三角形中,根据三角函数的定义得到球的半径是r,∴r /10 =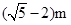 ,∴r=10
,∴r=10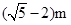 ,故半径为
,故半径为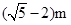 ,故选A.
,故选A.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
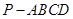 中,底面
中,底面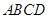 为矩形,
为矩形,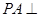 底面
底面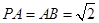 ,点
,点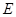 是棱
是棱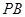 的中点.
的中点.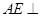 平面
平面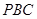 ;
;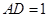 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值. 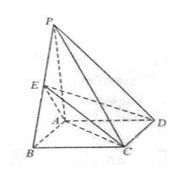
 中,平面
中,平面 平面
平面 ,
,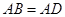 ,
,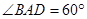 ,
,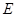 、
、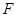 分别是
分别是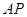 、
、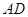 的中点。
的中点。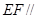 平面
平面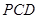 ;
;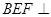 平面
平面 。(12分)
。(12分)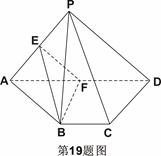
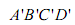 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.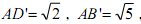 ,正方形的边长为
,正方形的边长为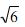 ,
, 的余弦值.
的余弦值.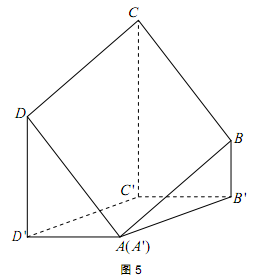
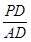 =
=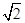 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.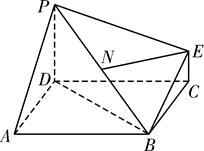
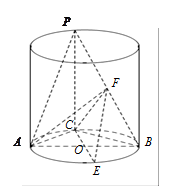
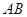 长度为
长度为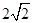 ,
,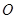 为底面圆心,正三角形
为底面圆心,正三角形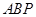 的一个顶点
的一个顶点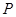 在上底面的圆周上,
在上底面的圆周上,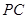 为圆柱的母线,
为圆柱的母线,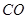 的延长线交
的延长线交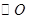 于点
于点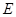 ,
, 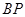 的中点为
的中点为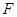 .
.
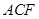 ;
;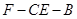 的正切值.
的正切值.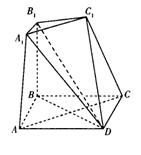
 中,
中, ,
, ,点
,点 在棱
在棱 上移动,问
上移动,问 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.