题目内容
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知过点
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知过点![]() 且斜率为1的直线
且斜率为1的直线![]() 与曲线
与曲线![]() :
:![]() (
(![]() 是参数)交于
是参数)交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 的中点为
的中点为![]() ,比较
,比较![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
【答案】(1)![]() ;
;![]() (2)
(2)![]() ,详见解析
,详见解析
【解析】
(1)将方程![]() 消参得到
消参得到![]() ,即为曲线C的普通方程,利用极坐标与直角坐标之间的转化关系,将
,即为曲线C的普通方程,利用极坐标与直角坐标之间的转化关系,将![]() 化为
化为![]() ,即为直线
,即为直线![]() 的直角坐标方程;
的直角坐标方程;
(2)联立![]() 消去y得
消去y得![]() ,设点
,设点![]() ,
,![]() ,则由中点公式,得点M的坐标是
,则由中点公式,得点M的坐标是![]() ,由韦达定理得到点M的坐标是(4,3),联立
,由韦达定理得到点M的坐标是(4,3),联立![]() ,求得点N的坐标是
,求得点N的坐标是![]() ,应用两点间距离公式和弦长公式求得
,应用两点间距离公式和弦长公式求得![]() 与
与![]() 的值,比较可得结果.
的值,比较可得结果.
(1)由![]() 得:
得:
![]() ,
,
故曲线C的普通方程是![]() ;
;
由![]() 及公式
及公式![]() 得
得![]() ,
,
故直线![]() 的直角坐标方程是
的直角坐标方程是![]() .
.
(2)因为直线![]() 过点
过点![]() 且斜率为1,
且斜率为1,
所以根据点斜式得,直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
曲线C:![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,
联立![]() 消去y得
消去y得![]() .
.
设点![]() ,
,![]() ,则由中点公式,得点M的坐标是
,则由中点公式,得点M的坐标是![]() .
.
由韦达定理,得![]() ,
,![]() ,所以
,所以![]() ,
,
所以点M的坐标是(4,3).
联立![]() 解得
解得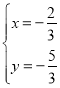 ,故点N的坐标是
,故点N的坐标是![]() .
.
所以由两点间的距离公式,得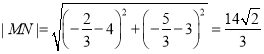 .
.
所以由弦长公式,得弦长![]() .
.
因为 ,
,
所以![]() .故
.故![]() .
.

练习册系列答案
相关题目