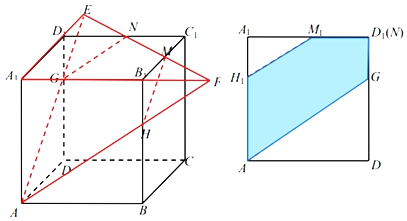
题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的弦长为3,直线
轴的弦长为3,直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为椭圆的右顶点.
为椭圆的右顶点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)用![]() ,
,![]() 分别表示
分别表示![]() 和
和![]() 的面积,求
的面积,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)6
;(Ⅱ)6
【解析】
(Ⅰ)利用条件,求得![]() ,
,![]() ,
,![]() 的值,从而得到椭圆的标准方程;
的值,从而得到椭圆的标准方程;
(Ⅱ)先分斜率存在和不存在两种情况讨论直线方程,当斜率不存在时,求出![]() 的值,当斜率存在时,设出直线方程
的值,当斜率存在时,设出直线方程![]() ,利用直线与圆相切,得到直线中
,利用直线与圆相切,得到直线中![]() ,
,![]() 的等量关系,然后将直线方程与椭圆方程进行联立,通过消元化简,得到根与系数的关系,求得直线与椭圆相交所得弦的长度及点到直线的距离,然后利用面积公式并通过换元,结合对勾函数的性质求得最小值.
的等量关系,然后将直线方程与椭圆方程进行联立,通过消元化简,得到根与系数的关系,求得直线与椭圆相交所得弦的长度及点到直线的距离,然后利用面积公式并通过换元,结合对勾函数的性质求得最小值.
解:(Ⅰ)由已知得![]() ,
,![]() ,结合
,结合![]() ,得
,得![]() ,
,![]()
所以椭圆的方程为![]() .
.
(Ⅱ)当![]() 斜率不存在时,
斜率不存在时,![]() ,得
,得![]() .
.
当![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]()
由![]() 与圆
与圆![]() 相切,得
相切,得![]() ,整理得
,整理得![]() (*)
(*)
将![]() 的方程与椭圆的方程联立得
的方程与椭圆的方程联立得![]()
所以![]() ,
,![]() .
.
则![]()
![]()
设![]() 为
为![]() 到直线
到直线![]() 的距离,则
的距离,则![]()
所以![]()
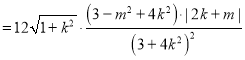
将(*)式代入得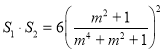
令![]()
所以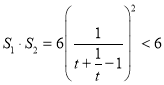 .
.
综上,![]() 的最大值为6.
的最大值为6.

练习册系列答案
相关题目