Question

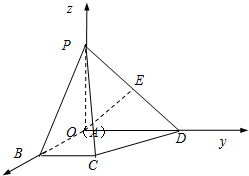在四棱锥P-ABCD中，底面ABCD是一直角梯形，PA⊥底面ABCD，∠BAD=90°，AD∥BC，AB=BC=1，AD=AP=2，E为PD的中点．以A为坐标原点，分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz．
（1）求

BE

的模；
（2）求＜

AE

，

DC

＞；（求异面直线AE与CD所成的角）；
（3）设

n

=（1，p，q），满足

n

⊥平面PCD，求

n

的坐标．

Answer 1

考点：空间向量的数量积运算

专题：空间向量及应用

分析：（1）由已知可得相关点的坐标，可得

BE

的坐标，由模长公式可得；
（2）由题意可得

AE

和

DC

的坐标，可得夹角余弦值，可得夹角；
（3）由垂直可得

n

•

PD

=2p-2q=0且 

n

•

CD

=-1+p=0，解方程组可得．

解答： 解：（1）由已知可得A（0，0，0），B（1，0，0），C（1，1，0），
D（0，2，0），P（0，0，2），∵E为PD的中点，∴E（0，1，1）．
∴|

BE

|=

(0-1)2+(1-0)2+(1-0)2

=

3

；
（2）

AE

=（0，1，1），

DC

=(1，-1，0)．
∴cos＜

AE

，

DC

＞=

AE • CD

| AE |•| CD |

=-

1

2 • 2

=-

1

2

，
∵＜

AE

，

DC

＞∈[0，π]，∴＜

AE

，

DC

＞=

2π

3

，即异面直线AE与CD所成的角为60°；
（3）∵

n

⊥平面PCD，∴

n

⊥PD，

n

⊥CD，
又 

n

=（1，p，q），

PD

=(0，2，-2)，

CD

=(-1，1，0)，
∴

n

•

PD

=2p-2q=0，

n

•

CD

=-1+p=0，
解得p=1且q=1，即

n

=（1，1，1）

点评：本题考查空间向量的数量积和模长公式，属基础题．