题目内容
 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若BC=2BF,且AF=4,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若BC=2BF,且AF=4,则此抛物线的方程为考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设出直线方程,与抛物线联立消去y得到关于x的一元二次方程,求得xAxB的表达式,根据BC=2BF确定关于p的等式,求得p,则抛物线方程可得.
解答:
解:设直线AC的方程为ky=x-
(k≠0)
联合抛物线y2=2px
消去y得x2-(1+2k2)px+
=0
∴xAxB=
①
依据抛物线的特性
|AF|=xA+
;|BF|=xB+
,
∴|CB|:|BF|=
(xB+
):p=|CB|:|CF|=2:3
∴xB=
②
∴①②联立求得xA=
,
∴|AF|=
+
=2p=3,
∴抛物线方程y2=3x.
故答案为:y2=3x.
| p |
| 2 |
联合抛物线y2=2px
消去y得x2-(1+2k2)px+
| p2 |
| 4 |
∴xAxB=
| p2 |
| 4 |
依据抛物线的特性
|AF|=xA+
| p |
| 2 |
| p |
| 2 |
∴|CB|:|BF|=
(xB+
| p |
| 2 |
∴xB=
| p |
| 6 |
∴①②联立求得xA=
| 3p |
| 2 |
∴|AF|=
| 3p |
| 2 |
| p |
| 2 |
∴抛物线方程y2=3x.
故答案为:y2=3x.
点评:本题主要考查了抛物线的简单性质.解决直线与抛物线的关系问题,一般考虑韦达定理的灵活运用.

练习册系列答案
相关题目
以茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )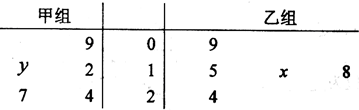

| A、5,2 | B、5,5 |
| C、8,5 | D、8,8 |
命题“若x2<1,则-1<x<1”的逆否命题是( )
| A、若x2≥1,则x≥1且x≤-1 |
| B、若-1<x<1,则x2<1 |
| C、若x>1或x<-1,则x2>1 |
| D、若x≥1或x≤-1,则x2≥1 |
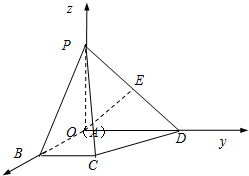 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz. 如图,设A为半径为1圆周上一定点,在圆周上等可能的任取一点B,则弦长|AB|超过
如图,设A为半径为1圆周上一定点,在圆周上等可能的任取一点B,则弦长|AB|超过