题目内容
曲线y2-x-2y=0在二阶矩阵M=
的作用下变换为曲线y2=x;
(Ⅰ)求实数a,b的值;
(Ⅱ)求M的逆矩阵M-1.
|
(Ⅰ)求实数a,b的值;
(Ⅱ)求M的逆矩阵M-1.
考点:变换、矩阵的相等
专题:计算题,矩阵和变换
分析:(Ⅰ)利用矩阵变换可得
,代入新曲线y2=x,即可求得实数a,b的值;
(Ⅱ)利用|M|=1及逆矩阵公式即可求得M的逆矩阵M-1.
|
(Ⅱ)利用|M|=1及逆矩阵公式即可求得M的逆矩阵M-1.
解答:
解:(Ⅰ)
=
,可得
代入新曲线y2=x,得(bx+ay)2=x+ay,即y2+2bxy+b2x2-x-ay=0
解得a2=2,b=0 …(4分)
(2)由|M|=1及逆矩阵公式得M-1=
…(7分)
|
|
|
|
代入新曲线y2=x,得(bx+ay)2=x+ay,即y2+2bxy+b2x2-x-ay=0
解得a2=2,b=0 …(4分)
(2)由|M|=1及逆矩阵公式得M-1=
|
点评:本题考查矩阵变换及逆矩阵公式的应用,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
如图,Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )

A、
| ||||
| B、1 | ||||
C、
| ||||
D、2
|
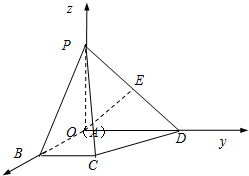 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz. 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队抽6人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队抽6人.