题目内容
在△ABC中,a,b,c分别为角A,B,C所对的边,若(a+b+c)(sinA+sinB-sinC)=asinB,又sinA=
,则sinB=( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:利用正弦定理求出A+B的余弦函数值,得到cos(A+B)=-
,继而求出sinB的值
| 1 |
| 2 |
解答:
解:由正弦定理可知(sinA+sinB+sinC)(sinA+sinB-sinC)=3sinAsinB
⇒(sinA+sinB)2-sin2C=3sinAsinB,
⇒sin2A+2sinAsinB+sin2B-sin2(A+B)=3sinAsinB,
⇒sin2A+sin2B-(sinAcosB+cosAsinB)2=sinAsinB,
⇒sin2A+sin2B-sin2A•cos2B-2sinAcosBcosAsinB-cos2A•sin2B=sinAsinB
⇒2sin2Asin2B-2sinAcosBsinBcosA=sinAsinB
⇒cosAcosB-sinAsinB=-
,
?cos(A+B)=-
,
∴A+B=120°,
∵sinA=
,
∴A=60°或120°(舍去),
∴B=60°
解得sinB=
故选:B
⇒(sinA+sinB)2-sin2C=3sinAsinB,
⇒sin2A+2sinAsinB+sin2B-sin2(A+B)=3sinAsinB,
⇒sin2A+sin2B-(sinAcosB+cosAsinB)2=sinAsinB,
⇒sin2A+sin2B-sin2A•cos2B-2sinAcosBcosAsinB-cos2A•sin2B=sinAsinB
⇒2sin2Asin2B-2sinAcosBsinBcosA=sinAsinB
⇒cosAcosB-sinAsinB=-
| 1 |
| 2 |
?cos(A+B)=-
| 1 |
| 2 |
∴A+B=120°,
∵sinA=
| ||
| 2 |
∴A=60°或120°(舍去),
∴B=60°
解得sinB=
| ||
| 2 |
故选:B
点评:本题考查正弦定理的应用,两角和与差的余弦函数的求法,注意解得范围,考查计算能力,另外利用正弦定理将条件中的角的正弦化为相应的边,属于中档题.

练习册系列答案
相关题目
以茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )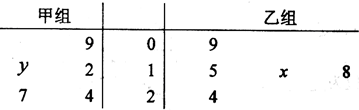

| A、5,2 | B、5,5 |
| C、8,5 | D、8,8 |
按如图所示的程序框图,在运行后输出的结果为( )


| A、7 | B、8 | C、9 | D、10 |
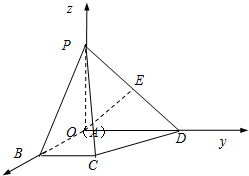 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.