题目内容
已知抛物线y2=4x的焦点为F,点A为该抛物线上一点,且∠OFA=120°(其中O为坐标原点),则线段AF的中点M到y轴的距离为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先确定抛物线的焦点坐标,准线方程,求出直线AF的方程,进而可求点A的坐标,由中点公式求解即可.
解答:
解:由题意,抛物线y2=4x的焦点坐标为F(1,0),准线方程为x=-1
∵∠AFO=120°(O为坐标原点),
∴kAF=
∴直线AF的方程为:y=
(x-1)
代入抛物线方程可得:3(x-1)2=4x
∴3x2-10x+3=0
∴x=3或x=
∵∠AFO=120°(O为坐标原点),
∴A(3,±2
),
∴线段AF的中点M到y轴的距离为
=2,
故答案为:2
∵∠AFO=120°(O为坐标原点),
∴kAF=
| 3 |
∴直线AF的方程为:y=
| 3 |
代入抛物线方程可得:3(x-1)2=4x
∴3x2-10x+3=0
∴x=3或x=
| 1 |
| 3 |
∵∠AFO=120°(O为坐标原点),
∴A(3,±2
| 2 |
∴线段AF的中点M到y轴的距离为
| 3+1 |
| 2 |
故答案为:2
点评:本题以抛物线的性质为载体,求出点A的坐标是关键,运用中点公式求解即可,难度不大.

练习册系列答案
相关题目
按如图所示的程序框图,在运行后输出的结果为( )


| A、7 | B、8 | C、9 | D、10 |
将函数y=cos(x-
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
个单位,则所得函数具有性质是( )
| 5π |
| 6 |
| π |
| 3 |
A、图象关于直线x=
| ||
B、图象关于(
| ||
C、图象关于直线x=
| ||
D、图象关于(
|
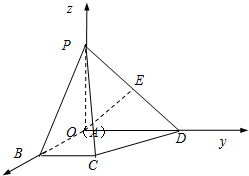 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.