题目内容
已知三棱柱ABC-A1B1C1的直观图和三视图如图所示,其主视图BB1A1A和侧视图A1ACC1均为矩形,其中AA1=4.俯视图△A1B1C1中,B1C1=4,A1C1=3,A1B1=5,D是AB的中点.
(1)求证:AC1∥平面CDB1;
(2)求异面直线AC1与B1C所成角的余弦值.
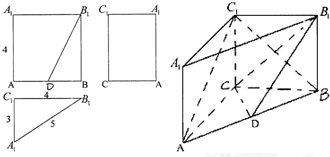
(1)求证:AC1∥平面CDB1;
(2)求异面直线AC1与B1C所成角的余弦值.

考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)设BC1与B1C相交与O,只要证明OD∥AC1,利用线面平行的判定定理证明;
(2)由三视图得到三棱柱的各棱长,通过(1)得到异面直线所成的角,然后由余弦定理求之.
(2)由三视图得到三棱柱的各棱长,通过(1)得到异面直线所成的角,然后由余弦定理求之.
解答:
(1)证明:设BC1与B1C相交与O,则O是B1C的中点,又D是AB的中点,
所以OD∥AC1,又OC?平面CDB1,AC1?平面CDB1,
所以AC1∥平面CDB1;
(2)解;由(1)得到OD∥AC1,异面直线AC1与B1C所成角的为∠COD或者∠B1OD,
又AA1=4,AC=3,BC=4,所以AB=5,OC=2
,所以OD=
,CD=
,
所以cos∠COD=
=
,
所以异面直线AC1与B1C所成角的余弦值
.
所以OD∥AC1,又OC?平面CDB1,AC1?平面CDB1,
所以AC1∥平面CDB1;
(2)解;由(1)得到OD∥AC1,异面直线AC1与B1C所成角的为∠COD或者∠B1OD,
又AA1=4,AC=3,BC=4,所以AB=5,OC=2
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
所以cos∠COD=
| OC2+OD2-CD2 |
| 2OC×OD |
| 2 |
| 5 |
所以异面直线AC1与B1C所成角的余弦值
| 2 |
| 5 |
点评:本题考查了几何体的三视图以及线面平行的判定和异面直线所成的角,正确将问题转化是关键.

练习册系列答案
相关题目
设函数f(x)=x3-2ex2+mx-lnx,记g(x)=
,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
| f(x) |
| x |
A、(-∞,e2+
| ||||
B、(0,e2+
| ||||
C、(e2+
| ||||
D、(-e2-
|
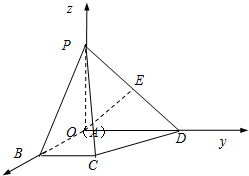 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E为PD的中点.以A为坐标原点,分别以AB、AD、AP为x轴、y轴、z轴建立如图所示空间直角坐标系O-xyz.