题目内容
14.求下列函数的值域:①y=sin(3x+$\frac{π}{6}$)(-$\frac{π}{6}≤x≤\frac{π}{6}$);
②y=2sin(2x+$\frac{π}{6}$),x$∈[-\frac{π}{6},\frac{π}{3}]$;
③y=sin($\frac{π}{4}-2x$)($-\frac{π}{4}≤x≤\frac{π}{4}$)
分析 求出函数的相位角的范围,结合正弦函数的图象和性质,可得相应正弦型函数的值域.
解答 解:①∵-$\frac{π}{6}≤x≤\frac{π}{6}$,
∴-$\frac{π}{3}$≤3x+$\frac{π}{6}$≤$\frac{2π}{3}$,
当3x+$\frac{π}{6}$=-$\frac{π}{3}$时,函数取最小值-$\frac{\sqrt{3}}{2}$,
当3x+$\frac{π}{6}$=$\frac{π}{2}$时,函数取最大值1,
故函数y=sin(3x+$\frac{π}{6}$)(-$\frac{π}{6}≤x≤\frac{π}{6}$)的值域为[-$\frac{\sqrt{3}}{2}$,1];
②∵x$∈[-\frac{π}{6},\frac{π}{3}]$,
∴2x+$\frac{π}{6}$$∈[-\frac{π}{6},\frac{5π}{6}]$,
当2x+$\frac{π}{6}$=-$\frac{π}{6}$时,函数取最小值-$\frac{1}{2}$,
当2x+$\frac{π}{6}$=$\frac{π}{2}$时,函数取最大值1,
故函数y=2sin(2x+$\frac{π}{6}$),x$∈[-\frac{π}{6},\frac{π}{3}]$的值域为[-$\frac{1}{2}$,1];
③∵$-\frac{π}{4}≤x≤\frac{π}{4}$,
∴$-\frac{π}{4}≤$$\frac{π}{4}-2x$$≤\frac{3π}{4}$,
当2x+$\frac{π}{6}$=-$\frac{π}{4}$时,函数取最小值-$\frac{\sqrt{2}}{2}$,
当2x+$\frac{π}{6}$=$\frac{π}{2}$时,函数取最大值1,
故函数y=sin($\frac{π}{4}-2x$)($-\frac{π}{4}≤x≤\frac{π}{4}$)的值域为[-$\frac{\sqrt{2}}{2}$,1];
点评 本题考查的知识点是正弦型函数的图象和性质,熟练掌握正弦型函数的图象和性质,是解答的关键.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案| A. | (-∞,2) | B. | (3,+∞) | C. | (2,3) | D. | (-∞,2)∪(3,+∞) |
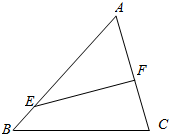 有一块三角形边角地,如图中△ABC,其中AB=8(百米),AC=6(百米),∠A=60°,某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中△AEF)供市民休闲,其中点E在边AB上,点F在边AC上,规划部门要求△AEF的面积占△ABC面积的一半,记△AEF的周长为l(百米).
有一块三角形边角地,如图中△ABC,其中AB=8(百米),AC=6(百米),∠A=60°,某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中△AEF)供市民休闲,其中点E在边AB上,点F在边AC上,规划部门要求△AEF的面积占△ABC面积的一半,记△AEF的周长为l(百米).