Question

19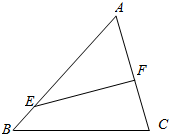．有一块三角形边角地，如图中△ABC，其中AB=8（百米），AC=6（百米），∠A=60°，某市为迎接2500年城庆，欲利用这块地修一个三角形形状的草坪（图中△AEF）供市民休闲，其中点E在边AB上，点F在边AC上，规划部门要求△AEF的面积占△ABC面积的一半，记△AEF的周长为l（百米）．
（1）如果要对草坪进行灌溉，需沿△AEF的三边安装水管，求水管总长度l的最小值；
（2）如果沿△AEF的三边修建休闲长廊，求长廊总长度l的最大值，并确定此时E、F的位置．

Answer 1

分析 （1）设AE=a，AF=b，利用△AEF的面积占△ABC面积的一半，求出ab=24，表示出水管总长度l，求导数，即可求水管总长度l的最小值；
（2）根据（1），1≥t≥4$\sqrt{6}$，即可求长廊总长度l的最大值，并确定此时E、F的位置．

解答 解：（1）由题意，设AE=a，AF=b，则$\frac{1}{2}absin60°$=$\frac{1}{2}•\frac{1}{2}•8•6•sin60°$，
∴ab=24，
EF²=a²+b²-2abcos60°=a²+b²-24=（a+b）²-72，
∴l=a+b+$\sqrt{（a+b）^{2}-72}$
b=$\frac{24}{a}$∈（0，6]，可得4≤a≤8
设t=a+b=a+$\frac{24}{a}$，∴11≥t≥4$\sqrt{6}$，
l=t+$\sqrt{{t}^{2}-72}$，
∴l′=1+$\frac{2t}{2\sqrt{{t}^{2}-72}}$＞0，
∴t=4$\sqrt{6}$，l_min=6$\sqrt{6}$（百米）．
（2）由（1），1≥t≥4$\sqrt{6}$，∴t=11，长廊总长度l的最大值为18（百米）．
此时a=8，b=3，即E在B点、F为AC的中点．

点评 本题考查利用数学知识解决实际问题，考查导数知识的运用，确定函数模型是关键．