题目内容
【题目】已知直线l1:2x﹣y+1=0,直线l2与l1关于直线y=﹣x对称,则直线l2的方程为( )
A.x﹣2y+1=0
B.x+2y+1=0
C.x﹣2y﹣1=0
D.x+2y﹣1=0
【答案】A
【解析】解:由 ![]() ,解得
,解得  , 即有l1和直线y=﹣x的交点A为(﹣
, 即有l1和直线y=﹣x的交点A为(﹣ ![]() ,
, ![]() ),
),
再在l1上取一点C(0,1),则点C关于直线y=﹣x的对称点B(m,n),
则有 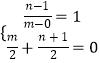 ,解得
,解得 ![]() ,
,
故点B(﹣1,0),
故AB的斜率为KAB= 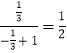 ,
,
由点斜式求得直线l1关于直线y=﹣x的对称的直线AB
即直线l2的方程为:y= ![]() (x+1),即x﹣2y+1=0.
(x+1),即x﹣2y+1=0.
故选:A.
先求得直线y=﹣x与直线l1的交点A的坐标,在直线l1上取一点C(0,1),求出点C关于直线y=﹣x的对称点B的坐标,可得AB的斜率,用点斜式求得对称直线l2的方程即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目