题目内容
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E是AA1的中点,求证: (Ⅰ)A1C∥平面BDE;
(Ⅱ)平面A1AC⊥平面BDE.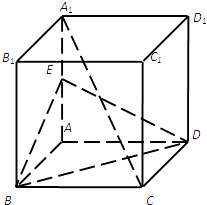
【答案】证明:(Ⅰ)连接AC交BD于O,连接EO, ∵E为AA1的中点,O为AC的中点
∴EO为△A1AC的中位线
∴EO∥A1C
又∵EO平面BDE,A1C平面BDE
∴A1C∥平面BDE;
(Ⅱ)∵AA1⊥平面ABCD,BD平面ABCD
∴AA1⊥BD
又∵四边形ABCD是正方形
∴AC⊥BD,
∵AA1∩AC=A,AA1、AC平面A1AC
∴BD⊥平面A1AC
又∵BD平面BDE
∴平面A1AC⊥平面BDE. 
【解析】(Ⅰ)连接AC交BD于O,连接EO,△A1AC中利用中位线,得EO∥A1C.再结合线面平行的判定定理,可得A1C∥平面BDE;(II)根据正方体的侧棱垂直于底面,结合线面垂直的定义,得到AA1⊥BD.再结合正方形的对角线互相垂直,得到AC⊥BD,从而得到BD⊥平面A1AC,最后利用面面垂直的判定定理,可以证出平面A1AC⊥平面BDE.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目