题目内容
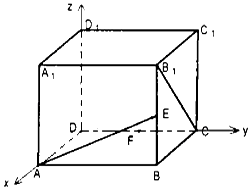
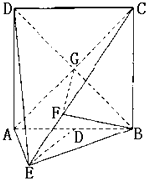
【题目】如图,直二面角D﹣AB﹣E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE. (Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B﹣AC﹣E的余弦值;
(Ⅲ)求点D到平面ACE的距离.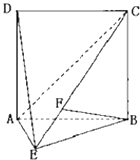
【答案】解:(Ⅰ)∵BF⊥平面ACE.∴BF⊥AE ∵二面角D﹣AB﹣E为直二面角.且CB⊥AB.
∴CB⊥平面ABE∴CB⊥AE
∵BF∩CB=B
∴AE⊥平面BCE
(Ⅱ)连接BD交AC交于G,连接FG
∵正方形ABCD边长为2.∴BG⊥AC,BG= ![]()
∵BF⊥平面ACE.由三垂线定理的逆定理得FG⊥AC.
∴∠BGF是二面B﹣AC﹣E的平面角
∵AE⊥平面BCE,∴AE⊥EC
又∵AE=EB,∴在等腰直角三角形AEB中,BE= ![]()
又∵Rt△BCE中,EC= ![]()
∴BF= ![]() =
= ![]()
∴Rt△BFG中sin∠BGF= ![]() =
= ![]()
∴二面角B﹣AC﹣E的正弦值等于 ![]()
(Ⅲ)过点E作EO⊥AB交AB于点O,OE=1
∵二面角D﹣AB﹣E为直二面角,∴EO⊥平面ABCD
设D到平面ACE的距离为h,由VD﹣ACE=VE﹣ACD , 可得h= 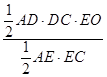 =
= ![]()
∴点D到平面ACE的距离为 ![]() .
. 
【解析】(Ⅰ)欲证AE⊥平面BCE,由题设条件知可先证BF⊥AE,CB⊥AE,再由线面垂直的判定定理得出线面垂直即可;(Ⅱ)求二面角B﹣AC﹣E的正弦值,需要先作角,连接BD交AC交于G,连接FG,可证得∠BGF是二面B﹣AC﹣E的平面角,在△BFG中求解即可;(Ⅲ)由题设,利用由VD﹣ACE=VE﹣ACD , 求点D到平面ACE的距离.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案