题目内容
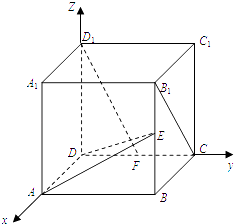
【题目】正方体ABCD﹣A1B1C1D1中,如图E、F分别是BB1 , CD的中点, 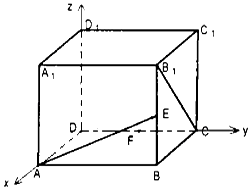
(1)求证:D1F⊥AE;
(2)求直线EF与CB1所成角的余弦值.
【答案】
(1)证明:依题意知D(0,0,0),A(2,0,0),F(0,1,0),E(2,2,1),A1(2,0,2),D1(0,0,2),
![]() =(0,0,1),
=(0,0,1), ![]() =(0,1,﹣2),
=(0,1,﹣2),
∴ ![]()
![]() =0,
=0,
∴AE⊥D1F;
∵AD⊥平面CDD1C1,D1F平面CDD1C1,
∴D1F⊥AD,
∵AE平面ADE,AD平面ADE,AE∩AD=A,
∴D1F⊥平面ADE
(2)解:依题意可知B1(1,1,1),C(0,1,0),F(0,1,0),E(2,2,1),
∴ ![]() =(2,1,1),
=(2,1,1), ![]() =(1,0,1),
=(1,0,1),
∴cos< ![]() ,
, ![]() >=
>= ![]() ,
,
∴异面直线EF和CB1所成的角余弦值为 ![]()
【解析】(1)依题意分别求得A,E,D1和F的坐标,求出 ![]() ,
, ![]() ,二者相乘等于0即可证明出AE⊥D1F进而根据线面垂直的性质证明出D1F⊥AD,最后根据线面垂直的判定定理证明出D1F⊥平面ADE.(2)分别求得
,二者相乘等于0即可证明出AE⊥D1F进而根据线面垂直的性质证明出D1F⊥AD,最后根据线面垂直的判定定理证明出D1F⊥平面ADE.(2)分别求得 ![]() =(2,1,1),
=(2,1,1), ![]() =(1,0,1),利用向量的夹角公式求得异面直线所成角的余弦值.
=(1,0,1),利用向量的夹角公式求得异面直线所成角的余弦值.
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.

练习册系列答案
相关题目