题目内容
【题目】某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图. 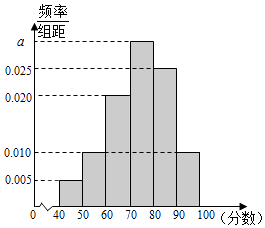
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
【答案】
(1)解:由于图中所有小矩形的面积之和等于1,
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1.
解得a=0.03
(2)解:根据频率分布直方图,成绩不低于6(0分)的频率为
1﹣10×(0.005+0.01)=0.85.
由于该校高一年级共有学生640人,利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于6(0分)的人数约为640×0.85=544人
(3)解:成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B.
成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.(7分)
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,
则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.(9分)
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:
(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.
所以所求概率为P(M)= ![]()
【解析】(1)根据阴影矩形的面积之和等于1,计算a的值;(2)首先计算成绩不低于60分的频率,即后四个小矩形的面积和,然后用640×频率计算人数;(3)若两名学生的学生成绩之差的绝对值不大于10,即两人是同一组的学生,那么首先计算两组的人数,并编号,并以编号的形式列出所有选取2人的基本事件的个数,同时计算同一组的两个人的所有基本事件的个数,最后相除得到概率.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案