题目内容
【题目】已知函数![]() ,其中
,其中![]() 为常数,
为常数,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上有意义,求实数
上有意义,求实数![]() 的取值范围。
的取值范围。
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:因为![]() 为奇函数,所以
为奇函数,所以![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,即
恒成立,即![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,故
恒成立,故![]() ,即
,即![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,故
恒成立,故![]() 得出
得出![]() 检验是否符合题意即可(2)若
检验是否符合题意即可(2)若![]() 在
在![]() 内恒有意义,则当
内恒有意义,则当![]() 时,有
时,有![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() ,从而
,从而![]() 在
在![]() 上恒成立,构造
上恒成立,构造 ![]() ,当
,当![]() 时,不合题意 , 当
时,不合题意 , 当![]() 时,同时限制端点即可.
时,同时限制端点即可.
试题解析:
(1)因为![]() 为奇函数,所以
为奇函数,所以![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,
恒成立,
即![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,
恒成立,
故![]() ,即
,即![]() 对定义域内的任意
对定义域内的任意![]() 恒成立,
恒成立,
故![]() ,即
,即![]()
当![]() 时,
时, ![]() 为奇函数,满足条件;
为奇函数,满足条件;
当![]() 时,
时, ![]() 无意义,故不成立。
无意义,故不成立。
综上, ![]()
(2)若![]() 在
在![]() 内恒有意义,则当
内恒有意义,则当![]() 时,有
时,有![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() ,从而
,从而![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则
当![]() 时,不合题意
时,不合题意
当![]() 时,
时, 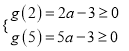 ,解得
,解得![]() ,
,
所以,实数![]() 的取值范围是
的取值范围是![]()

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
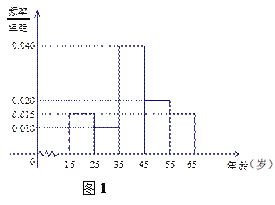
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
观看方式 年龄(岁) | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
![]()
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: 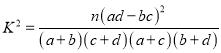
【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为![]() .
.
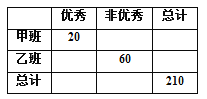
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附: 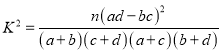
【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |