题目内容
【题目】为加快新能源汽车产业发展，推进节能减排，国家对消费者购买新能源汽车给予补贴，其中对纯电动乘用车补贴标准如表：
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R（公里） | ||
100≤R＜180 | 180≤R＜280 | ＜280 | |
纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
某校研究性学习小组，从汽车市场上随机选取了M辆纯电动乘用车，根据其续驶里程R（单次充电后能行驶的最大里程）作出了频率与频数的统计表：
分组 | 频数 | 频率 |
100≤R＜180 | 3 | 0.3 |
180≤R＜280 | 6 | x |
R≥280 | y | z |
合计 | M | 1 |
（1）求x、y、z、M的值；
（2）若从这M辆纯电动乘用车任选3辆，求选到的3辆车续驶里程都不低于180公里的概率；
（3）如果以频率作为概率，若某家庭在某汽车销售公司购买了2辆纯电动乘用车，设该家庭获得的补贴为X（单位：万元），求X的分布列和数学期望值E（X）．
【答案】
（1）解：由题意得：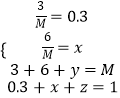 
，
解得x=0.6，y=1，z=0.1，M=10．
（2）解：从这M辆纯电动乘用车任选3辆，
基本事件总数n= 
=120，
10辆车中，有7辆车续驶里程不低于180公里，
选到的3辆车续驶里程都不低于180公里包含的基本事件个数m= 
=35，
∴选到的3辆车续驶里程都不低于180公里的概率p= 
= 
．
（3）解：由题意知X的可能取值为5，6.5，8，8.5，10，12，
P（X=5）=0.32=0.09，
P（X=6.5）= 
，
P（X=8）=0.62=0.36，
P（X=8.5）= 
=0.06，
P（X=10）= 
，
P（X=12）=0.12=0.01，
∴X的分布列为：
X | 5 | 6.5 | 8 | 8.5 | 10 | 12 |
P | 0.09 | 0.36 | 0.36 | 0.06 | 0.12 | 0.01 |
E（X）=5×0.09+6.5×0.36+8×0.36+8.5×0.06+10×0.12+12×0.01=7.5．
【解析】（1）由频率与频数的统计表列出方程组，能求出x、y、z、M的值．（2）从这M辆纯电动乘用车任选3辆，基本事件总数n= =120，10辆车中，有7辆车续驶里程不低于180公里，选到的3辆车续驶里程都不低于180公里包含的基本事件个数m= =35，由此能求出选到的3辆车续驶里程都不低于180公里的概率．（3）由题意知X的可能取值为5，6.5，8，8.5，10，12，分别求出相应的概率，由此能求出X的分布列和E（X）．
【考点精析】根据题目的已知条件，利用离散型随机变量及其分布列的相关知识可以得到问题的答案，需要掌握在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．
