题目内容
对于方程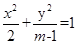 (
( )的曲线C,下列说法错误的是
)的曲线C,下列说法错误的是
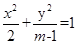 (
( )的曲线C,下列说法错误的是
)的曲线C,下列说法错误的是A.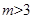 时,曲线C是焦点在y轴上的椭圆 时,曲线C是焦点在y轴上的椭圆 | B.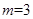 时,曲线C是圆 时,曲线C是圆 |
C.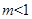 时,曲线C是双曲线 时,曲线C是双曲线 | D.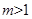 时,曲线C是椭圆 时,曲线C是椭圆 |
D
试题分析:A.
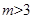 时,
时,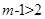 ,所以曲线C表示焦点在y轴上的椭圆,正确;B.
,所以曲线C表示焦点在y轴上的椭圆,正确;B.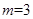 时,曲线C为
时,曲线C为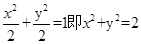 ,因此曲线C表示圆,正确;C.
,因此曲线C表示圆,正确;C.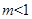 时,
时,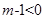 ,所以曲线C是双曲线 ,正确; D.
,所以曲线C是双曲线 ,正确; D.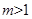 时,曲线C是椭圆,错误,因为当
时,曲线C是椭圆,错误,因为当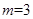 时,曲线C是圆。
时,曲线C是圆。点评:熟练掌握判断椭圆、双曲线以及圆的方程的特点。方程
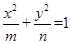 ,当
,当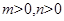 且
且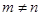 时表示椭圆;(当
时表示椭圆;(当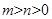 时,表示焦点在x轴上的椭圆;当
时,表示焦点在x轴上的椭圆;当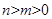 时表示焦点在y轴上的椭圆。)当
时表示焦点在y轴上的椭圆。)当 时,表示双曲线;当
时,表示双曲线;当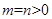 时,表示圆。
时,表示圆。
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
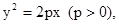 过焦点
过焦点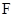 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;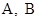 两点, 存在定点
两点, 存在定点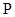 , 使得
, 使得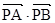 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明. 中,若
中,若
 右顶点,则常数
右顶点,则常数 .
. +
+ =1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
=1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d. ,求k的值;
,求k的值; ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.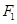 ,
, 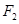 是椭圆
是椭圆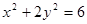 的两个焦点,点
的两个焦点,点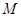 在此椭圆上且
在此椭圆上且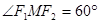 ,则
,则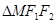 的面积等于( )
的面积等于( )
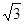

 的离心率为
的离心率为 ,且过点(
,且过点( ),
), 与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.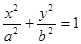 (a>
(a>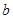 )中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角
)中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角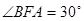 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



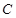 :
: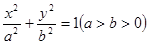 的左、右顶点分别
的左、右顶点分别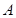 、
、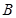 ,椭圆过点
,椭圆过点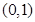 且离心率
且离心率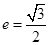 .
.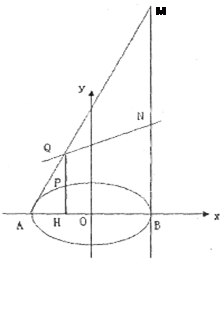
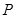 作
作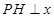 轴,
轴,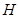 为垂足,延长
为垂足,延长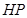 到点
到点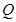 ,且
,且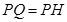 ,过点
,过点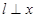 轴,连结
轴,连结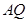 并延长交直线
并延长交直线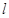 于点
于点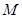 ,线段
,线段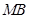 的中点记为点
的中点记为点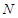 .
.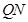 与以
与以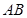 为直径的圆
为直径的圆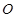 的位置关系, 并证明.
的位置关系, 并证明.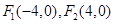 ,动点
,动点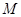 满足条件:
满足条件: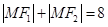 ,则点
,则点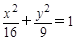
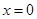
 (
(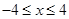 )
)