题目内容
(I) 已知抛物线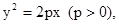 过焦点
过焦点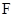 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;
(Ⅱ)由 (Ⅰ) 可知: 过抛物线的焦点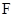 的动直线 l 交抛物线于
的动直线 l 交抛物线于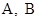 两点, 存在定点
两点, 存在定点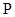 , 使得
, 使得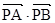 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.
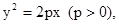 过焦点
过焦点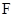 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;(Ⅱ)由 (Ⅰ) 可知: 过抛物线的焦点
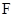 的动直线 l 交抛物线于
的动直线 l 交抛物线于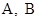 两点, 存在定点
两点, 存在定点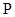 , 使得
, 使得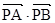 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.(I) 见解析;
(II) 过椭圆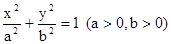 的一个焦点
的一个焦点 的动直线l交椭圆于
的动直线l交椭圆于 、
、 两点, 存在定点
两点, 存在定点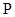 , 使
, 使 为定值.
为定值.
(II) 过椭圆
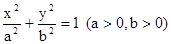 的一个焦点
的一个焦点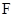 的动直线l交椭圆于
的动直线l交椭圆于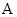 、
、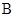 两点, 存在定点
两点, 存在定点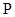 , 使
, 使 为定值.
为定值. 本题主要考查抛物线的基本性质以及直线与圆锥曲线的综合问题.在解决直线与圆锥曲线综合问题时,常把直线方程与圆锥曲线方程联立.
(1)先讨论出当直线l垂直于x轴时, 的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入
的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入
计算即可得到结论
(2)先写出类似结论,再根据第一问求
的方法即可得到结论.(注意要分直线斜率存在和不存在两种情况讨论).
解: (I) 若直线l垂直于x轴, 则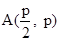 ,
, 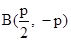 .
.
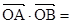
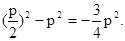 ……………2分
……………2分
若直线l不垂直于x轴, 设其方程为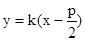 ,
, 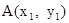
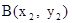 .
.
由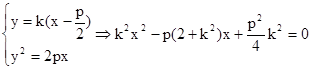
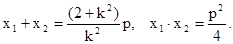 ……………4分
……………4分
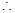

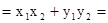
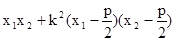
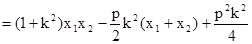
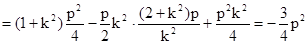 .
.
综上,
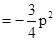 为定值. ……………6分
为定值. ……………6分
(II) 关于椭圆有类似的结论: 过椭圆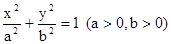 的一个焦点
的一个焦点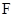 的动直线l交椭圆于
的动直线l交椭圆于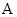 、
、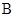 两点, 存在定点
两点, 存在定点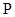 , 使
, 使 为定值. ……………7分
为定值. ……………7分
证明: 不妨设直线l过椭圆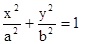 的右焦点
的右焦点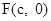
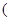 其中
其中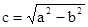
若直线l不垂直于x轴, 则设其方程为: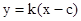 ,
, 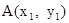
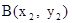 .
.
由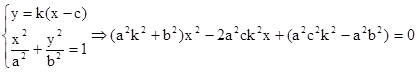 得:
得:
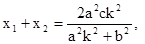
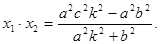 ……………9分
……………9分
由对称性可知, 设点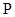 在x轴上, 其坐标为
在x轴上, 其坐标为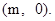
所以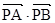
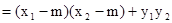
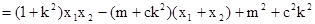
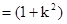
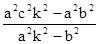
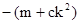
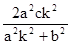
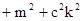
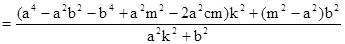
要使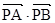 为定值,
为定值,
只要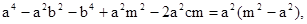
即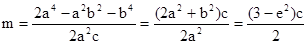
此时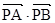
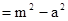
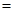
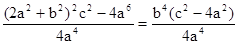 ……………12分
……………12分
若直线l垂直于x轴, 则其方程为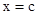 ,
, 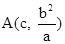 ,
, 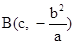 .
.
取点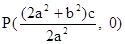 ,
,
有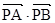
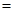
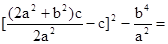
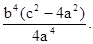 ……………13分
……………13分
综上, 过焦点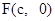 的任意直线l交椭圆于
的任意直线l交椭圆于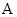 、
、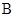 两点, 存在定点
两点, 存在定点
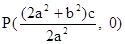
使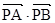
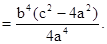 为定值. ……………14分
为定值. ……………14分
(1)先讨论出当直线l垂直于x轴时,
 的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入
的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入
计算即可得到结论
(2)先写出类似结论,再根据第一问求

的方法即可得到结论.(注意要分直线斜率存在和不存在两种情况讨论).
解: (I) 若直线l垂直于x轴, 则
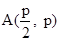 ,
, 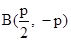 .
.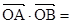
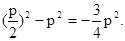 ……………2分
……………2分若直线l不垂直于x轴, 设其方程为
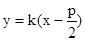 ,
, 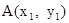
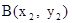 .
.由
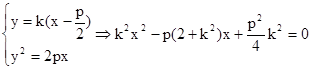
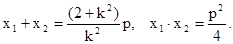 ……………4分
……………4分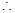

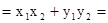
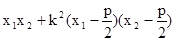
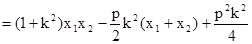
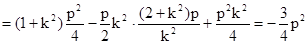 .
.综上,

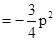 为定值. ……………6分
为定值. ……………6分(II) 关于椭圆有类似的结论: 过椭圆
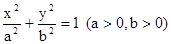 的一个焦点
的一个焦点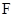 的动直线l交椭圆于
的动直线l交椭圆于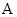 、
、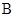 两点, 存在定点
两点, 存在定点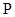 , 使
, 使 为定值. ……………7分
为定值. ……………7分证明: 不妨设直线l过椭圆
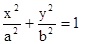 的右焦点
的右焦点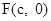
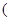 其中
其中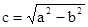
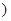
若直线l不垂直于x轴, 则设其方程为:
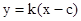 ,
, 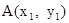
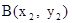 .
.由
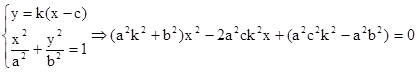 得:
得: 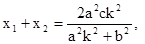
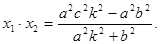 ……………9分
……………9分由对称性可知, 设点
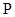 在x轴上, 其坐标为
在x轴上, 其坐标为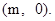
所以
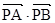
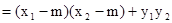
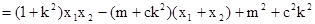
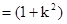
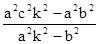
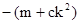
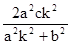
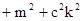
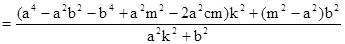
要使
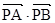 为定值,
为定值, 只要
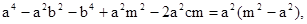
即
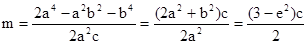
此时
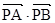
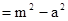
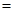
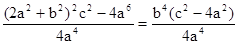 ……………12分
……………12分若直线l垂直于x轴, 则其方程为
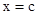 ,
, 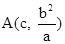 ,
, 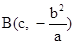 .
.取点
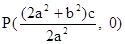 ,
,有
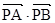
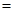
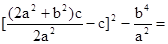
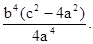 ……………13分
……………13分综上, 过焦点
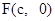 的任意直线l交椭圆于
的任意直线l交椭圆于 、
、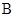 两点, 存在定点
两点, 存在定点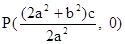
使
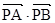
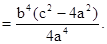 为定值. ……………14分
为定值. ……………14分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
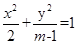 (
( )的曲线C,下列说法错误的是
)的曲线C,下列说法错误的是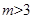 时,曲线C是焦点在y轴上的椭圆
时,曲线C是焦点在y轴上的椭圆 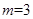 时,曲线C是圆
时,曲线C是圆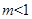 时,曲线C是双曲线
时,曲线C是双曲线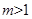 时,曲线C是椭圆
时,曲线C是椭圆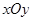 中,已知椭圆
中,已知椭圆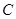 :
: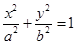 (
(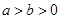 )的左焦点为
)的左焦点为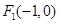 ,且点
,且点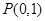 在
在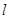 的斜率为2且经过椭圆
的斜率为2且经过椭圆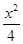 +
+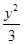 =1的右焦点到直线y=
=1的右焦点到直线y=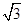 x的距离是 ( )
x的距离是 ( )
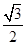
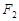 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,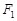 的直线MF1是圆
的直线MF1是圆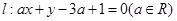 ,椭圆
,椭圆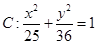 ,直线
,直线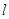 与椭圆
与椭圆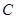 的公共点的个数为( )
的公共点的个数为( ) ,离心率
,离心率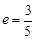 ,焦点在
,焦点在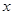 轴上的椭圆标准方程是 ( )
轴上的椭圆标准方程是 ( )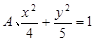
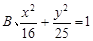
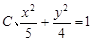
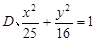
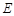 的普通方程为
的普通方程为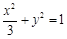
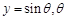 为参数,求椭圆
为参数,求椭圆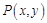 是椭圆
是椭圆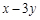 的取值范围.
的取值范围. 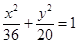 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: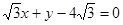 且
且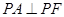 .
.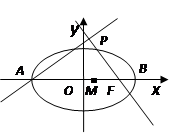
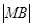 ,求椭圆上的点到点M的距离d的最小值.
,求椭圆上的点到点M的距离d的最小值.