题目内容
已知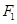 ,
, 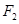 是椭圆
是椭圆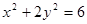 的两个焦点,点
的两个焦点,点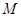 在此椭圆上且
在此椭圆上且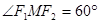 ,则
,则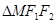 的面积等于( )
的面积等于( )
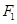 ,
, 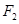 是椭圆
是椭圆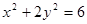 的两个焦点,点
的两个焦点,点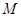 在此椭圆上且
在此椭圆上且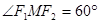 ,则
,则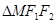 的面积等于( )
的面积等于( )A. | B.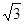 | C.2 | D. |
B
试题分析:
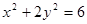 即
即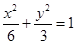 ,所以a=
,所以a=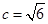 ,
,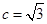 ,设
,设 =t,则在
=t,则在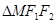 中,由余弦定理得,
中,由余弦定理得,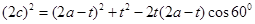 ,解得
,解得点评:中档题,涉及椭圆的“焦点三角形”问题,往往要运用椭圆的定义。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
题目内容
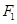 ,
, 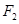 是椭圆
是椭圆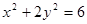 的两个焦点,点
的两个焦点,点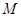 在此椭圆上且
在此椭圆上且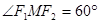 ,则
,则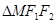 的面积等于( )
的面积等于( )A. | B.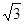 | C.2 | D. |
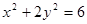 即
即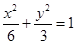 ,所以a=
,所以a=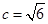 ,
,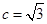 ,设
,设 =t,则在
=t,则在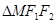 中,由余弦定理得,
中,由余弦定理得,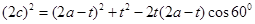 ,解得
,解得
 科学实验活动册系列答案
科学实验活动册系列答案