题目内容
在平面直角坐标系 中,若
中,若
 右顶点,则常数
右顶点,则常数 .
.
 中,若
中,若
 右顶点,则常数
右顶点,则常数 .
.3
因为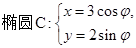 ,所以
,所以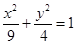 ,右顶点为(3,0),因为直线
,右顶点为(3,0),因为直线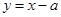 ,将点坐标带入直线方程可得
,将点坐标带入直线方程可得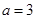 .
.
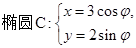 ,所以
,所以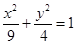 ,右顶点为(3,0),因为直线
,右顶点为(3,0),因为直线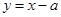 ,将点坐标带入直线方程可得
,将点坐标带入直线方程可得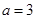 .
.
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
题目内容
 中,若
中,若
 右顶点,则常数
右顶点,则常数 .
.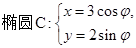 ,所以
,所以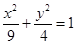 ,右顶点为(3,0),因为直线
,右顶点为(3,0),因为直线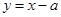 ,将点坐标带入直线方程可得
,将点坐标带入直线方程可得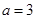 .
.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案