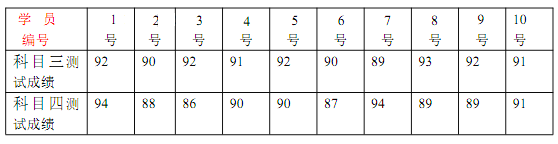
题目内容
【题目】河道上有一抛物线型拱桥，在正常水位时，拱圈最高点距水面8m，拱圈内水面宽24m，一条船在水面以上部分高6.5m，船顶部宽6m．
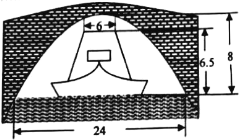
（1）试建立适当的直角坐标系，求拱桥所在的抛物线的标准方程；
（2）近日水位暴涨了1.54m，为此，必须加重船载，降低船身，才能通过桥洞，试问：船身至少应该降低多少?（精确到0.1m）
【答案】（1）直角坐标系见解析，拱桥所在的抛物线方程是
（2）0.6m
【解析】
（1）根据图形建立直角坐标系，设出拱桥所在的抛物线方程，设拱桥与水面两交点分别为
，
，由坐标系可知A,B两点的坐标，将其中一个代入抛物线方程，即可得；（2）根据船顶宽6m，可知船顶距离拱桥最高点的极限高度h，再由
，可知船身应降低高度。
解：（1）设抛物线型拱桥与水面两交点分别为，，以
垂直平分线为
轴，拱圈最高点
为坐标原点，建立平面直角坐标系，
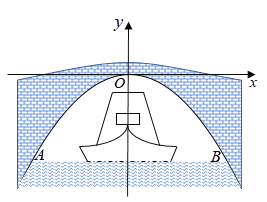
则
，
，
设拱桥所在的抛物线方程为
，
因点在抛物线上，代入解得
，
故拱桥所在的抛物线方程是．
（2）因，故当
时，
，
故当水位暴涨1.54m后，船身至少应降低
，
因精确到0.1m，故船身应降低0.6m．
答：船身应降低0.6m，才能安全通过桥洞．
练习册系列答案
口算能手系列答案
相关题目
