Question

【题目】已知椭圆C：（）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.

（1）求椭圆C的标准方程；

（2）设F为椭圆C的左焦点，T为直线上任意一点，过F作TF的垂线交椭圆C于点P，Q.

（i）证明：OT平分线段PQ（其中O为坐标原点）；

（ii）当最小时，求点T的坐标.

Answer 1

【答案】(1)；（2）证明见解析，

【解析】

（1）由题意，又，由此可求出的值，从而求得椭圆的方程.（2）椭圆方程化为.设PQ的方程为，代入椭圆方程得：.（ⅰ）设PQ的中点为，求出，只要，即证得OT平分线段PQ.（ⅱ）可用表示出PQ，TF可得：化简得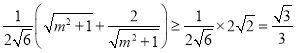：.再根据取等号的条件，可得T的坐标.

（1），又.

（2）椭圆方程化为.

（ⅰ）设PQ的方程为，代入椭圆方程得：.

设PQ的中点为，则

又TF的方程为，则得，

所以，即OT过PQ的中点，即OT平分线段PQ.

（ⅱ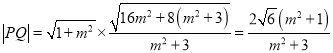），又，所以

.

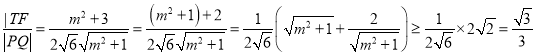当时取等号，此时T的坐标为.