题目内容
【题目】设![]() .
.
(1)证明: ![]() 在
在![]() 上单调递减;
上单调递减;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)第(1)问,直接求导,证明0<x<1时, f(x)<0 .(2)第(2)问,
分0<a≤![]() 和
和![]() <a<1两种情况证明,每一种情况都是先通过求单调性再求函数的最小值大于1.
<a<1两种情况证明,每一种情况都是先通过求单调性再求函数的最小值大于1.
试题解析:
(1)f(x)=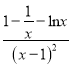 .
.
令h(x)=1-![]() -lnx,则h(x)=
-lnx,则h(x)=![]() ,x>0,
,x>0,
所以0<x<1时,h(x)>0,h(x)单调递增,
又h(1)=0,所以h(x)<0,
即f(x)<0,所以f(x)单调递减.
(2)g(x)=axlna+axa-1=a(ax-1lna+xa-1),
当0<a≤![]() 时,lna≤-1,所以ax-1lna+xa-1≤xa-1-ax-1.
时,lna≤-1,所以ax-1lna+xa-1≤xa-1-ax-1.
由(Ⅰ)得![]() ,所以(a-1)lnx<(x-1)lna,即xa-1<ax-1,
,所以(a-1)lnx<(x-1)lna,即xa-1<ax-1,
所以g(x)<0,g(x)在(a,1)上单调递减,
即g(x)>g(1)=a+1>1.
当![]() <a<1时,-1<lna<0.
<a<1时,-1<lna<0.
令t(x)=ax-xlna-1,0<a<x<1,则t(x)=axlna-lna=(ax-1)lna>0,
所以t(x)在(0,1)上单调递增,即t(x)>t(0)=0,
所以ax>xlna+1
所以g(x)=ax+xa>xa+xlna+1=x(xa-1+lna)+1>x(1+lna)+1>1.
综上,g(x)>1.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】随着互联网经济不断发展,网上开店销售农产品的人群越来越多,网上交易额也逐年增加,某一农户农产品连续五年的网银交易额统计表,如下所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网上交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,农户将上表的数据进行了处理,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程.求出![]() 关于
关于![]() 的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
(附:在线性回归方程![]() 中,
中,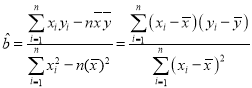 ,
,![]() )
)