题目内容
1.已知数列{an}中,a1=2,且(n+1)an-(n-1)an-1=0(n≥2),则an=$\frac{4}{n(n+1)}$.分析 通过(n+1)an-(n-1)an-1=0(n≥2)得出后一项与前一项的比,进而利用累乘法计算即得结论.
解答 解:∵(n+1)an-(n-1)an-1=0(n≥2),
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$,
∴$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n-2}{n}$,$\frac{{a}_{n-2}}{{a}_{n-3}}$=$\frac{n-3}{n-1}$,…,$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{3}$,
累乘得:$\frac{{a}_{n}}{{a}_{1}}$=$\frac{2}{n(n+1)}$,
又∵a1=2,
∴an=$\frac{4}{n(n+1)}$,
故答案为:$\frac{4}{n(n+1)}$.
点评 本题考查数列的通项,利用累乘法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则f(x)<0的解集为( )
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-2,0)∪(0,2) |
16.已知数列{an}的首项a1=1,且an+1=2an+1,则这个数列的第五项为( )
| A. | 31 | B. | 15 | C. | 11 | D. | 9 |
6.几何体的三视图和相关数据如图所示,则该几何体的体积为( )
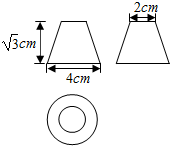

| A. | $\frac{{7\sqrt{3}π}}{3}$ | B. | $\frac{{8\sqrt{3}π}}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}{(m-3)x+4m,x≥0}\\{{m}^{x},x<0}\end{array}$,若对任意实数a≠b都有$\frac{f(a)-f(b)}{a-b}$<0,则实数m的取值范围是( )
| A. | 0<m<1 | B. | 0<m≤$\frac{1}{4}$ | C. | $\frac{1}{4}$≤m<1 | D. | m<3 |
11.已知$\frac{sinθ+cosθ}{sinθ-cosθ}$=2,则sinθcosθ的值是( )
| A. | $\frac{3}{4}$ | B. | ±$\frac{3}{10}$ | C. | $\frac{3}{10}$ | D. | -$\frac{3}{10}$ |