ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÄłč«ËŸÎȘÈ·¶šÏÂÒ»Äê¶ÈͶÈëÄłÖÖČúÆ·”ÄĐûŽ«·ŃŁŹĐèÁËœâÄêĐûŽ«·Ń![]() Łš”„λŁșÍòÔȘŁ©¶ÔÄêÏúÊÛÁż
Łš”„λŁșÍòÔȘŁ©¶ÔÄêÏúÊÛÁż![]() Łš”„λŁș¶ÖŁ©”ÄÓ°ÏìŁŹ¶ÔœüÁùÄê”ÄÄêĐûŽ«·Ń
Łš”„λŁș¶ÖŁ©”ÄÓ°ÏìŁŹ¶ÔœüÁùÄê”ÄÄêĐûŽ«·Ń![]() șÍÄêÏúÊÛÁż
șÍÄêÏúÊÛÁż![]() (
(![]() )”ÄÊęŸĘŚśÁËłőČœÍłŒÆŁŹ”Ă”œÈçÏÂÊęŸĘŁș
)”ÄÊęŸĘŚśÁËłőČœÍłŒÆŁŹ”Ă”œÈçÏÂÊęŸĘŁș
Äê·ĘŁš | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
ÄêĐûŽ«·Ń | 23 | 25 | 27 | 29 | 32 | 35 |
ÄêÏúÊÛÁż | 11 | 21 | 24 | 66 | 115 | 325 |
Łš1Ł©žùŸĘÉą”ăÍŒĆжÏ![]() Óë
Óë![]() ŁŹÄÄÒ»žöžüÊÊșÏŚśÎȘÄêÏúÊÛÁż
ŁŹÄÄÒ»žöžüÊÊșÏŚśÎȘÄêÏúÊÛÁż![]() Łš¶ÖŁ©ÓëčŰÓÚĐûŽ«·Ń
Łš¶ÖŁ©ÓëčŰÓÚĐûŽ«·Ń![]() ŁšÍòÔȘŁ©”Ä»Űčé·œłÌÀàĐÍŁ»
ŁšÍòÔȘŁ©”Ä»Űčé·œłÌÀàĐÍŁ»
Łš2Ł©č涚”±ČúÆ·”ÄÄêÏúÊÛÁż![]() Łš¶ÖŁ©ÓëÄêĐûŽ«·Ń
Łš¶ÖŁ©ÓëÄêĐûŽ«·Ń![]() ŁšÍòÔȘŁ©”ıÈÖ”ŽóÓÚ1ʱŁŹÈÏÎȘžĂÄêЧÒæÁŒșĂŁŹÏÖŽÓŐâ6ÄêÖĐÈÎŃĄ3ÄêŁŹŒÇÆäÖĐŃĄ”œĐ§ÒæÁŒșĂ”ÄÊęÁżÎȘ
ŁšÍòÔȘŁ©”ıÈÖ”ŽóÓÚ1ʱŁŹÈÏÎȘžĂÄêЧÒæÁŒșĂŁŹÏÖŽÓŐâ6ÄêÖĐÈÎŃĄ3ÄêŁŹŒÇÆäÖĐŃĄ”œĐ§ÒæÁŒșĂ”ÄÊęÁżÎȘ![]() ŁŹÊÔÇó
ŁŹÊÔÇó![]() ”ÄËùÓĐÈĄÖ”ÇéżöŒ°¶ÔÓŠ”ÄžĆÂÊŁ»
”ÄËùÓĐÈĄÖ”ÇéżöŒ°¶ÔÓŠ”ÄžĆÂÊŁ»
Łš3Ł©žùŸĘÆ”ÂÊ·ÖČŒÖ±·œÍŒÖĐÇółöŃù±ŸÊęŸĘÆœŸùÊę”ÄËŒÏë·œ·šŁŹÇó![]() ”ÄÆœŸùÊę.
”ÄÆœŸùÊę.
ĄŸŽđ°žĄżŁš1Ł©Éą”ăÍŒŒûœâÎöŁ»Łš2Ł©![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() Ł»Łš3Ł©
Ł»Łš3Ł©![]() .
.
ĄŸœâÎöĄż·ÖÎöŁșŁš1Ł©žùŸĘÉą”ăÍŒŁŹŒŽżÉĆĐ¶Ïłö.
Łš2Ł©ÓɱíÖĐÊęŸĘżÉÖȘŁŹĐ§ÒæÁŒșĂÓĐ3ÄêŁŹÉèЧÒæÁŒșĂÄêÎȘAĄąBșÍCŁŹÆäËûÄê·ĘÎȘ1Ąą2șÍ3ŁŹĂ¶ŸÙ·šÁĐłöÈ«ČżżÉÄÜœáčûčČ20ÖÖŁŹÔÙ·Ö±đÈ·¶šÆäÖĐÂúŚăЧÒæÁŒșĂ”ÄÊęÁżÎȘ![]() Äê”ÄÖÖÀàŁŹœű¶űÇółö¶ÔÓŠ”ÄžĆÂÊŁ»
Äê”ÄÖÖÀàŁŹœű¶űÇółö¶ÔÓŠ”ÄžĆÂÊŁ»
Łš3Ł©žùŸĘÆ”ÂÊ·ÖČŒÖ±·œÍŒÇóŃù±ŸÊęŸĘÆœŸùÊę”Ä·œ·š”ĂŁș![]() ŁŹŒŽżÉÇółö
ŁŹŒŽżÉÇółö![]() ”ÄÆœŸùÊę.
”ÄÆœŸùÊę.
ÏêœâŁșœâŁșŁš1Ł©»łöÉą”ăÍŒÒŚÖȘŁŹ·œłÌ![]() ±ÈœÏÊÊÒËŁ»
±ÈœÏÊÊÒËŁ»
Łš2Ł©ÒŚ”ĂŒŽ6ÄêÖĐÓĐ3ÄêÊÇĄ°Đ§ÒæÁŒșĂÄêĄ±,
Éè6ÄêÖĐЧÒæșĂÄê·Ę·Ö±đÎȘŁșA,B,CŁŹÆäËûÄê·ĘÎȘ1,2,3Ôò6ÄêÖĐŃĄ3Äê”ÄȻ͏œáčûÓĐŁș
ABC,AB1,AB2,AB3,AC1,AC2,AC3,BC1,BC2,BC3,A12,A13,A23,B12,B13,B23,C12,C13,C23ŁŹ123čČ20ÖÖŁ»
ÆäÖĐ![]() ÓĐ1ÖÖŁŹËùÒÔ
ÓĐ1ÖÖŁŹËùÒÔ![]() ŁŹ
ŁŹ
ÆäÖĐ![]() ÓĐ9ÖÖŁŹËùÒÔ
ÓĐ9ÖÖŁŹËùÒÔ![]() ,
,
ÆäÖĐ![]() ÓĐ9ÖÖŁŹËùÒÔ
ÓĐ9ÖÖŁŹËùÒÔ![]() ,
,
ÆäÖĐ![]() ÓĐ1ÖÖŁŹËùÒÔ
ÓĐ1ÖÖŁŹËùÒÔ![]() ,
,
Łš3Ł©žùŸĘÆ”ÂÊ·ÖČŒÖ±·œÍŒÇóŃù±ŸÊęŸĘÆœŸùÊę”Ä·œ·š”ĂŁș
![]() ŁŹ
ŁŹ
ŽđŁș![]() ”ÄÆœŸùÊę
”ÄÆœŸùÊę![]() .
.

ĄŸÌâÄżĄżÒŃÖȘČúÆ·![]() ”ÄÖÊÁżČÉÓĂŚÛșÏÖž±êÖ”
”ÄÖÊÁżČÉÓĂŚÛșÏÖž±êÖ”![]() œűĐĐșâÁżŁŹ
œűĐĐșâÁżŁŹ![]() ÎȘÒ»”ÈÆ·Ł»
ÎȘÒ»”ÈÆ·Ł»![]() ÎȘ¶ț”ÈÆ·Ł»
ÎȘ¶ț”ÈÆ·Ł»![]() ÎȘÈę”ÈÆ·.ÎÒÊĐÒ»ŒÒ耳§ŚŒ±žčșœűĐÂĐÍÉ豞ÒÔÌážßÉúČúČúÆ·
ÎȘÈę”ÈÆ·.ÎÒÊĐÒ»ŒÒ耳§ŚŒ±žčșœűĐÂĐÍÉ豞ÒÔÌážßÉúČúČúÆ·![]() ”ÄЧÒæŁŹÔÚÄłč©ÓŠÉÌÌáč©”ÄÉ豞ÖĐÈÎŃĄÒ»žöÊÔÓĂŁŹÉúČúÁËÒ»ĆúČúÆ·ČąÍłŒÆÏàčŰÊęŸĘŁŹ”Ă”œÆ”ÂÊ·ÖČŒÖ±·œÍŒŁș
”ÄЧÒæŁŹÔÚÄłč©ÓŠÉÌÌáč©”ÄÉ豞ÖĐÈÎŃĄÒ»žöÊÔÓĂŁŹÉúČúÁËÒ»ĆúČúÆ·ČąÍłŒÆÏàčŰÊęŸĘŁŹ”Ă”œÆ”ÂÊ·ÖČŒÖ±·œÍŒŁș
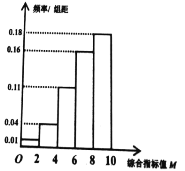
Łš1Ł©čÀŒÆžĂĐÂĐÍÉ豞ÉúČú”ÄČúÆ·![]() ÎȘ¶ț”ÈÆ·”ÄžĆÂÊŁ»
ÎȘ¶ț”ÈÆ·”ÄžĆÂÊŁ»
Łš2Ł©žùŸĘŐâŒÒ耳§”ÄŒÇÂŒŁŹČúÆ·žś”ȎΔÄÏúÊÛÂÊŁšÄł”ÈŽÎČúÆ·ÏúÁżÓëÆä¶ÔÓŠČúÁż”ıÈÖ”Ł©Œ°”„ŒțÊÛŒÛÇéżöÈçÏÂŁș
Ò»”ÈÆ· | ¶ț”ÈÆ· | Èę”ÈÆ· | |
ÏúÊÛÂÊ |
|
|
|
”„ŒțÊÛŒÛ |
|
|
|
žùŸĘÒÔÍù”ÄÏúÊÛ·œ°žŁŹÎŽÊÛłö”ÄČúÆ·ÍłÒ»°ŽÔÊی۔Ä![]() È«ČżŽŠÀíÍê.ÒŃÖȘžĂ耳§ÈÏčșžĂĐÂĐÍÉ豞”ÄÇ°ÌáÌőŒțÊÇŁŹžĂĐÂĐÍÉ豞ÉúČú”ÄČúÆ·ÍŹÊ±ÂúŚăÏÂÁĐÁœžöÌőŒțŁș
È«ČżŽŠÀíÍê.ÒŃÖȘžĂ耳§ÈÏčșžĂĐÂĐÍÉ豞”ÄÇ°ÌáÌőŒțÊÇŁŹžĂĐÂĐÍÉ豞ÉúČú”ÄČúÆ·ÍŹÊ±ÂúŚăÏÂÁĐÁœžöÌőŒțŁș
ąÙŚÛșÏÖž±êÖ””ÄÆœŸùÊęȻХÓÚ![]() ŁšÍŹÒ»ŚéÖĐ”ÄÊęŸĘÓÞÌéÇűŒä”ÄÖĐ”ăÖ”ŚśŽú±íŁ©Ł»
ŁšÍŹÒ»ŚéÖĐ”ÄÊęŸĘÓÞÌéÇűŒä”ÄÖĐ”ăÖ”ŚśŽú±íŁ©Ł»
ąÚ”„ŒțÆœŸùÀûÈó֔Ȼ”ÍÓÚ![]() .
.
ÈôžĂĐÂĐÍÉ豞ÉúČú”ÄČúÆ·![]() ”ijɱŸÎȘ
”ijɱŸÎȘ![]() ÔȘ/ŒțŁŹÔÂČúÁżÎȘ
ÔȘ/ŒțŁŹÔÂČúÁżÎȘ![]() ŒțŁŹÔÚÏúÊÛ·œ°žČ»±ä”ÄÇéżöÏÂŁŹžùŸĘÒÔÉÏÍŒ±íÊęŸĘŁŹ·ÖÎöžĂĐÂĐÍÉ豞ÊÇ·ńŽï”œžĂ耳§”ÄÈÏčșÌőŒț.
ŒțŁŹÔÚÏúÊÛ·œ°žČ»±ä”ÄÇéżöÏÂŁŹžùŸĘÒÔÉÏÍŒ±íÊęŸĘŁŹ·ÖÎöžĂĐÂĐÍÉ豞ÊÇ·ńŽï”œžĂ耳§”ÄÈÏčșÌőŒț.


